Scalable Gaussian Process Hyperparameter Optimization via Coverage Regularization

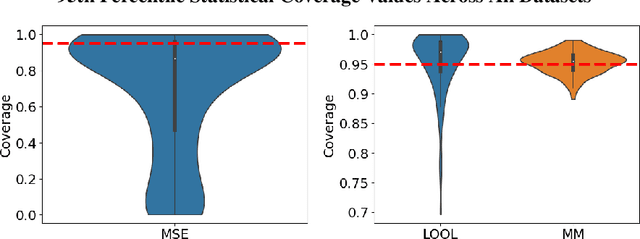
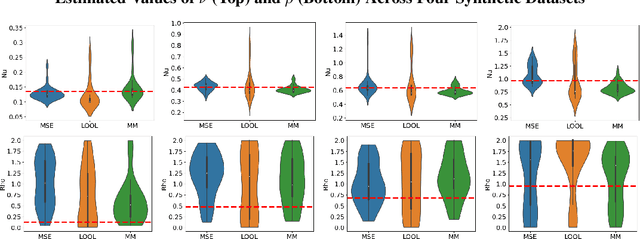
Gaussian processes (GPs) are Bayesian non-parametric models popular in a variety of applications due to their accuracy and native uncertainty quantification (UQ). Tuning GP hyperparameters is critical to ensure the validity of prediction accuracy and uncertainty; uniquely estimating multiple hyperparameters in, e.g. the Matern kernel can also be a significant challenge. Moreover, training GPs on large-scale datasets is a highly active area of research: traditional maximum likelihood hyperparameter training requires quadratic memory to form the covariance matrix and has cubic training complexity. To address the scalable hyperparameter tuning problem, we present a novel algorithm which estimates the smoothness and length-scale parameters in the Matern kernel in order to improve robustness of the resulting prediction uncertainties. Using novel loss functions similar to those in conformal prediction algorithms in the computational framework provided by the hyperparameter estimation algorithm MuyGPs, we achieve improved UQ over leave-one-out likelihood maximization while maintaining a high degree of scalability as demonstrated in numerical experiments.

Light curve completion and forecasting using fast and scalable Gaussian processes (MuyGPs)

Temporal variations of apparent magnitude, called light curves, are observational statistics of interest captured by telescopes over long periods of time. Light curves afford the exploration of Space Domain Awareness (SDA) objectives such as object identification or pose estimation as latent variable inference problems. Ground-based observations from commercial off the shelf (COTS) cameras remain inexpensive compared to higher precision instruments, however, limited sensor availability combined with noisier observations can produce gappy time-series data that can be difficult to model. These external factors confound the automated exploitation of light curves, which makes light curve prediction and extrapolation a crucial problem for applications. Traditionally, image or time-series completion problems have been approached with diffusion-based or exemplar-based methods. More recently, Deep Neural Networks (DNNs) have become the tool of choice due to their empirical success at learning complex nonlinear embeddings. However, DNNs often require large training data that are not necessarily available when looking at unique features of a light curve of a single satellite. In this paper, we present a novel approach to predicting missing and future data points of light curves using Gaussian Processes (GPs). GPs are non-linear probabilistic models that infer posterior distributions over functions and naturally quantify uncertainty. However, the cubic scaling of GP inference and training is a major barrier to their adoption in applications. In particular, a single light curve can feature hundreds of thousands of observations, which is well beyond the practical realization limits of a conventional GP on a single machine. Consequently, we employ MuyGPs, a scalable framework for hyperparameter estimation of GP models that uses nearest neighbors sparsification and local cross-validation. MuyGPs...

Fast Gaussian Process Posterior Mean Prediction via Local Cross Validation and Precomputation

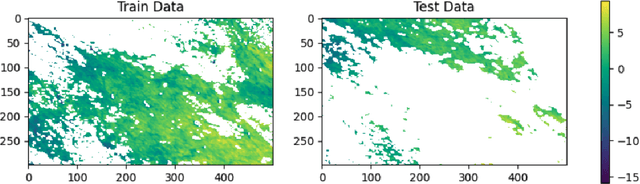
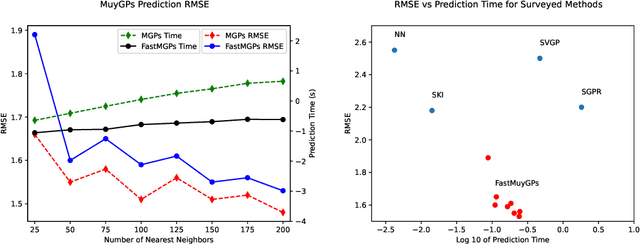
Gaussian processes (GPs) are Bayesian non-parametric models useful in a myriad of applications. Despite their popularity, the cost of GP predictions (quadratic storage and cubic complexity with respect to the number of training points) remains a hurdle in applying GPs to large data. We present a fast posterior mean prediction algorithm called FastMuyGPs to address this shortcoming. FastMuyGPs is based upon the MuyGPs hyperparameter estimation algorithm and utilizes a combination of leave-one-out cross-validation, batching, nearest neighbors sparsification, and precomputation to provide scalable, fast GP prediction. We demonstrate several benchmarks wherein FastMuyGPs prediction attains superior accuracy and competitive or superior runtime to both deep neural networks and state-of-the-art scalable GP algorithms.