Correspondence of NNGP Kernel and the Matern Kernel

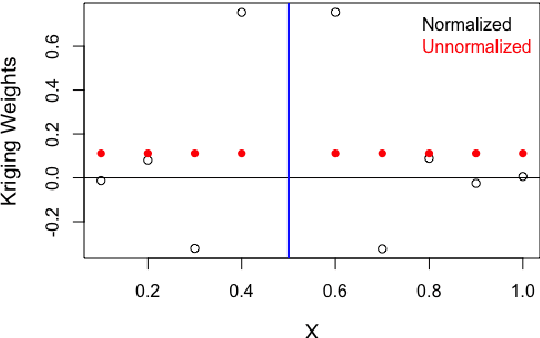
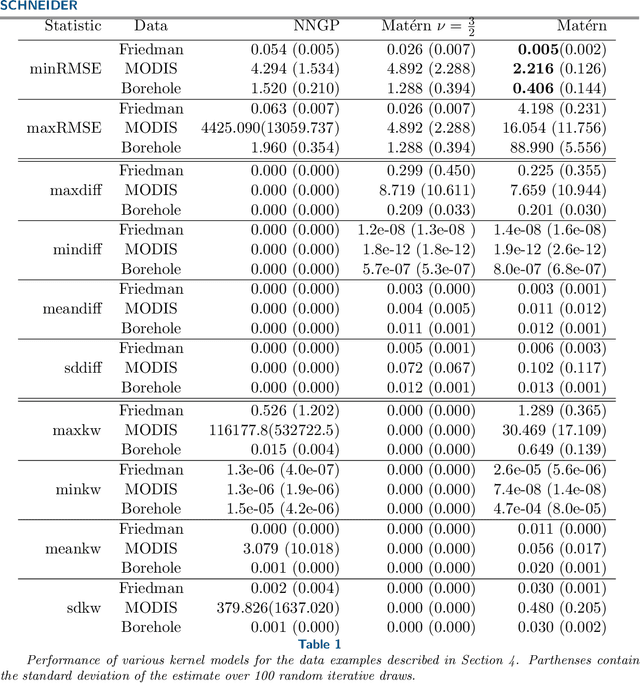
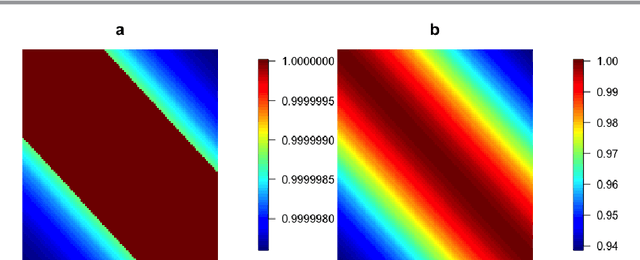
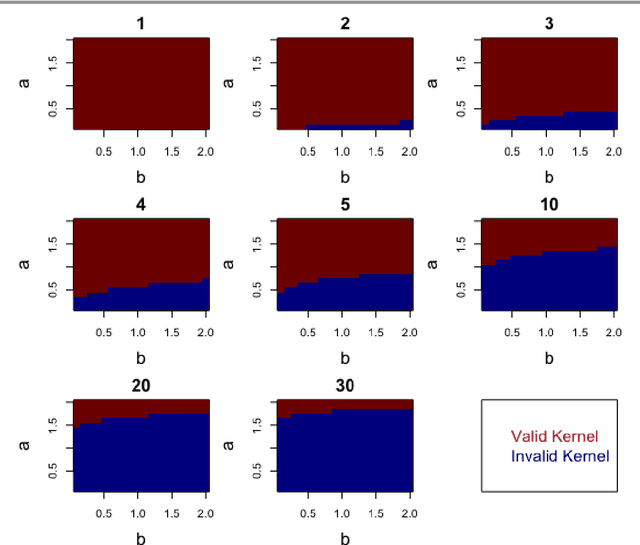
Kernels representing limiting cases of neural network architectures have recently gained popularity. However, the application and performance of these new kernels compared to existing options, such as the Matern kernel, is not well studied. We take a practical approach to explore the neural network Gaussian process (NNGP) kernel and its application to data in Gaussian process regression. We first demonstrate the necessity of normalization to produce valid NNGP kernels and explore related numerical challenges. We further demonstrate that the predictions from this model are quite inflexible, and therefore do not vary much over the valid hyperparameter sets. We then demonstrate a surprising result that the predictions given from the NNGP kernel correspond closely to those given by the Matern kernel under specific circumstances, which suggests a deep similarity between overparameterized deep neural networks and the Matern kernel. Finally, we demonstrate the performance of the NNGP kernel as compared to the Matern kernel on three benchmark data cases, and we conclude that for its flexibility and practical performance, the Matern kernel is preferred to the novel NNGP in practical applications.

Scalable Gaussian Process Hyperparameter Optimization via Coverage Regularization

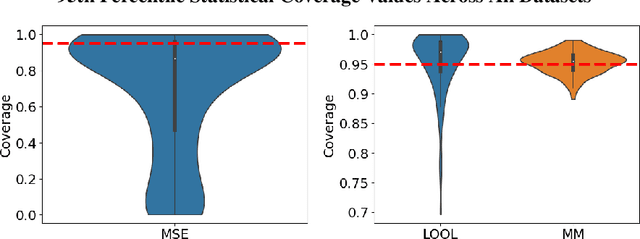
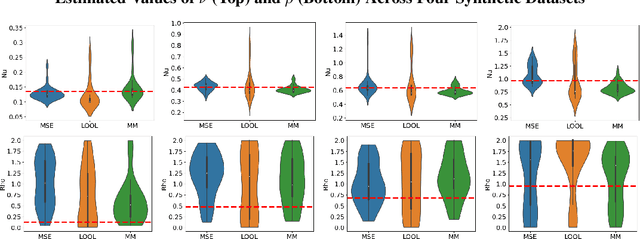
Gaussian processes (GPs) are Bayesian non-parametric models popular in a variety of applications due to their accuracy and native uncertainty quantification (UQ). Tuning GP hyperparameters is critical to ensure the validity of prediction accuracy and uncertainty; uniquely estimating multiple hyperparameters in, e.g. the Matern kernel can also be a significant challenge. Moreover, training GPs on large-scale datasets is a highly active area of research: traditional maximum likelihood hyperparameter training requires quadratic memory to form the covariance matrix and has cubic training complexity. To address the scalable hyperparameter tuning problem, we present a novel algorithm which estimates the smoothness and length-scale parameters in the Matern kernel in order to improve robustness of the resulting prediction uncertainties. Using novel loss functions similar to those in conformal prediction algorithms in the computational framework provided by the hyperparameter estimation algorithm MuyGPs, we achieve improved UQ over leave-one-out likelihood maximization while maintaining a high degree of scalability as demonstrated in numerical experiments.

Fast Gaussian Process Posterior Mean Prediction via Local Cross Validation and Precomputation

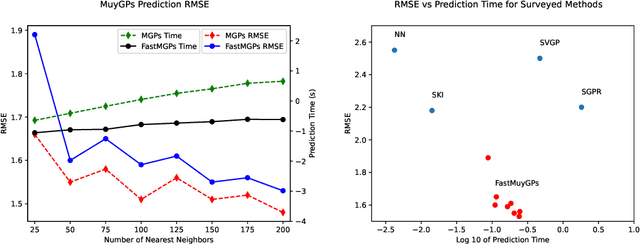
Gaussian processes (GPs) are Bayesian non-parametric models useful in a myriad of applications. Despite their popularity, the cost of GP predictions (quadratic storage and cubic complexity with respect to the number of training points) remains a hurdle in applying GPs to large data. We present a fast posterior mean prediction algorithm called FastMuyGPs to address this shortcoming. FastMuyGPs is based upon the MuyGPs hyperparameter estimation algorithm and utilizes a combination of leave-one-out cross-validation, batching, nearest neighbors sparsification, and precomputation to provide scalable, fast GP prediction. We demonstrate several benchmarks wherein FastMuyGPs prediction attains superior accuracy and competitive or superior runtime to both deep neural networks and state-of-the-art scalable GP algorithms.

MuyGPs: Scalable Gaussian Process Hyperparameter Estimation Using Local Cross-Validation

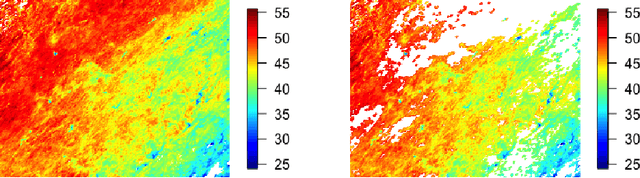
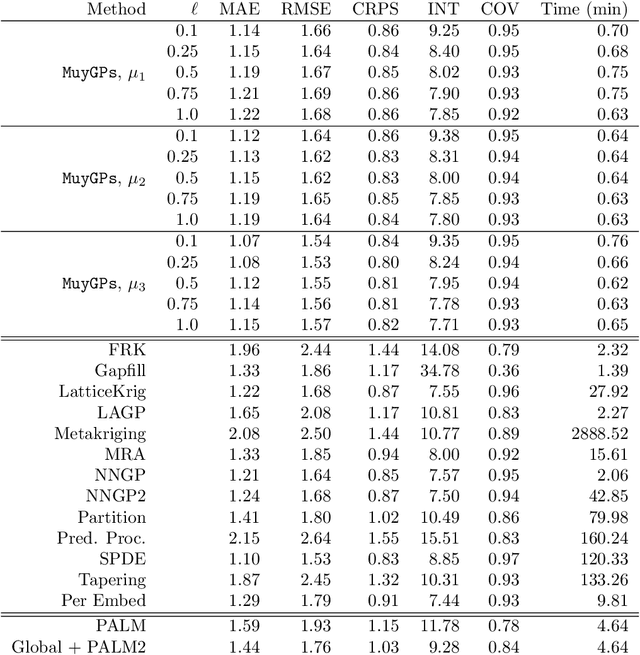
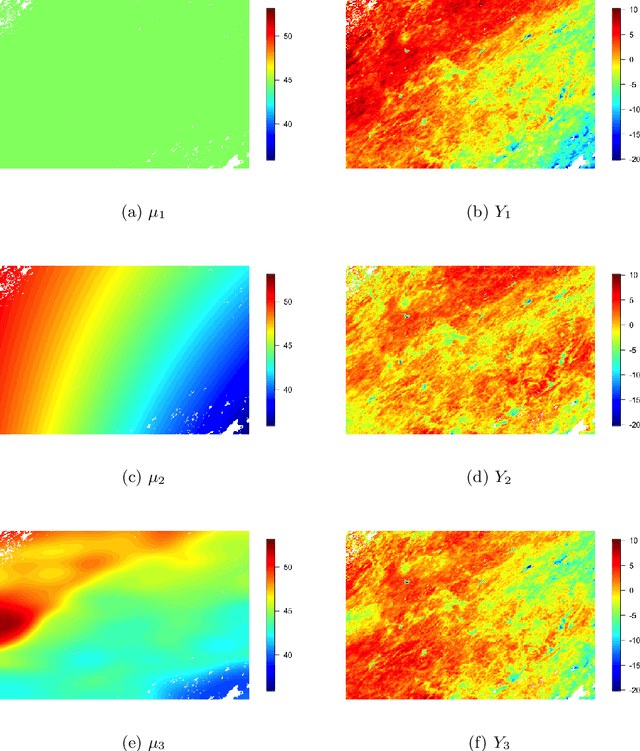
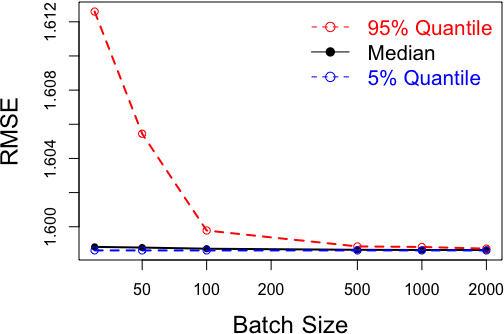
Gaussian processes (GPs) are non-linear probabilistic models popular in many applications. However, na\"ive GP realizations require quadratic memory to store the covariance matrix and cubic computation to perform inference or evaluate the likelihood function. These bottlenecks have driven much investment in the development of approximate GP alternatives that scale to the large data sizes common in modern data-driven applications. We present in this manuscript MuyGPs, a novel efficient GP hyperparameter estimation method. MuyGPs builds upon prior methods that take advantage of the nearest neighbors structure of the data, and uses leave-one-out cross-validation to optimize covariance (kernel) hyperparameters without realizing a possibly expensive likelihood. We describe our model and methods in detail, and compare our implementations against the state-of-the-art competitors in a benchmark spatial statistics problem. We show that our method outperforms all known competitors both in terms of time-to-solution and the root mean squared error of the predictions.