MuyGPs: Scalable Gaussian Process Hyperparameter Estimation Using Local Cross-Validation
Paper and Code
Apr 29, 2021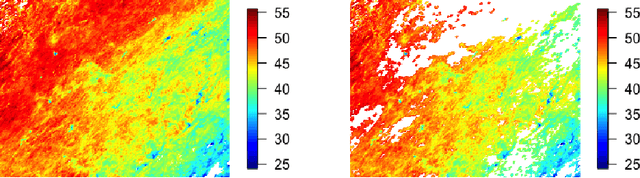
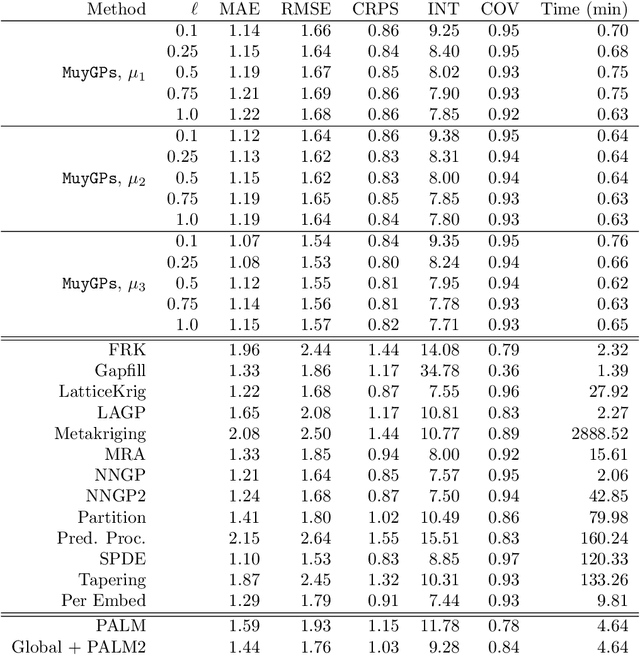
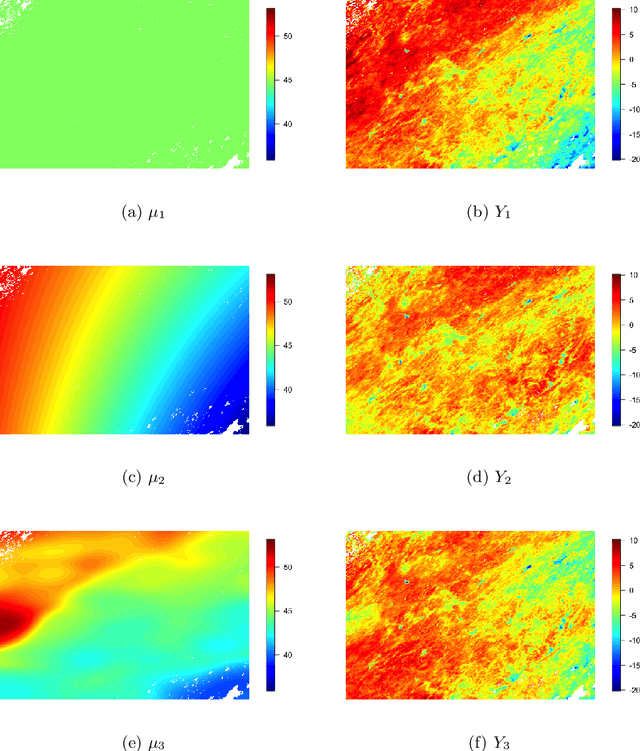
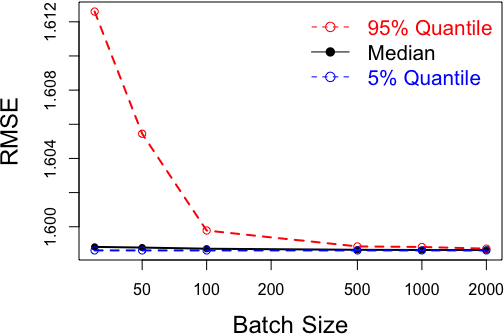
Gaussian processes (GPs) are non-linear probabilistic models popular in many applications. However, na\"ive GP realizations require quadratic memory to store the covariance matrix and cubic computation to perform inference or evaluate the likelihood function. These bottlenecks have driven much investment in the development of approximate GP alternatives that scale to the large data sizes common in modern data-driven applications. We present in this manuscript MuyGPs, a novel efficient GP hyperparameter estimation method. MuyGPs builds upon prior methods that take advantage of the nearest neighbors structure of the data, and uses leave-one-out cross-validation to optimize covariance (kernel) hyperparameters without realizing a possibly expensive likelihood. We describe our model and methods in detail, and compare our implementations against the state-of-the-art competitors in a benchmark spatial statistics problem. We show that our method outperforms all known competitors both in terms of time-to-solution and the root mean squared error of the predictions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge