Correspondence of NNGP Kernel and the Matern Kernel

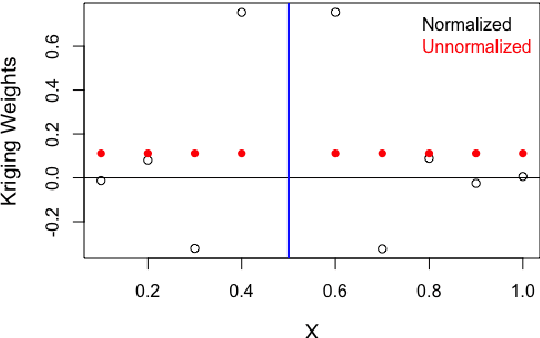
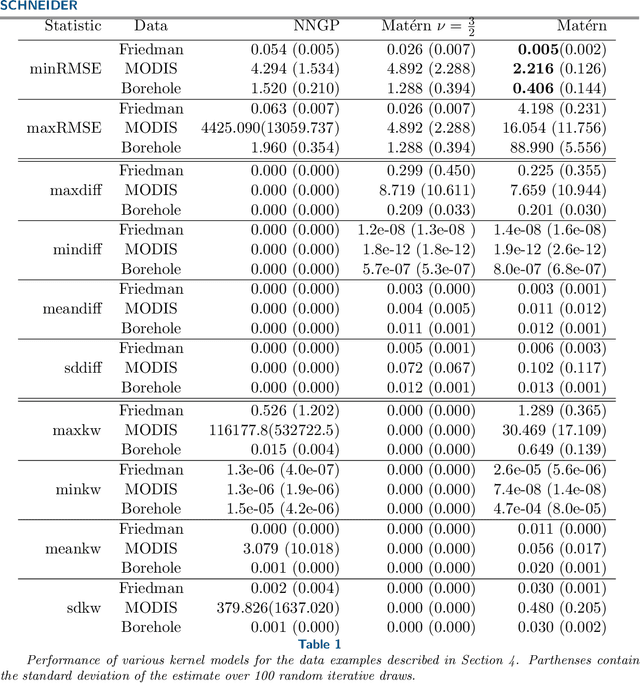
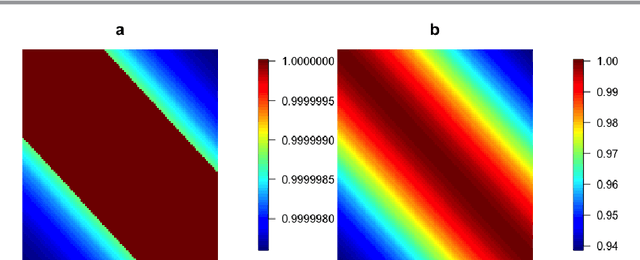
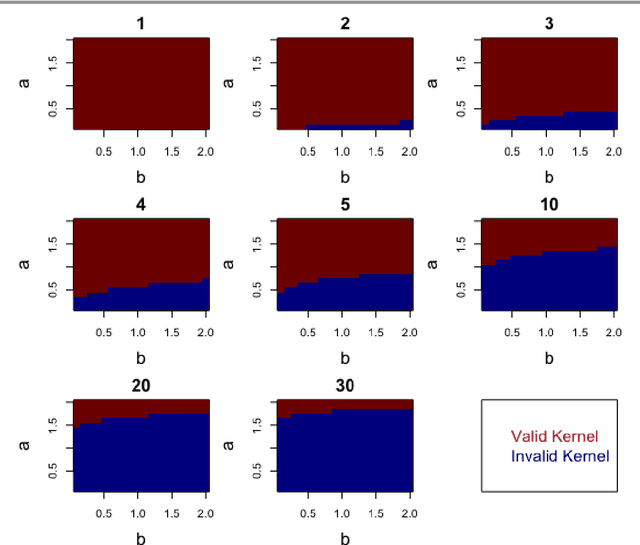
Kernels representing limiting cases of neural network architectures have recently gained popularity. However, the application and performance of these new kernels compared to existing options, such as the Matern kernel, is not well studied. We take a practical approach to explore the neural network Gaussian process (NNGP) kernel and its application to data in Gaussian process regression. We first demonstrate the necessity of normalization to produce valid NNGP kernels and explore related numerical challenges. We further demonstrate that the predictions from this model are quite inflexible, and therefore do not vary much over the valid hyperparameter sets. We then demonstrate a surprising result that the predictions given from the NNGP kernel correspond closely to those given by the Matern kernel under specific circumstances, which suggests a deep similarity between overparameterized deep neural networks and the Matern kernel. Finally, we demonstrate the performance of the NNGP kernel as compared to the Matern kernel on three benchmark data cases, and we conclude that for its flexibility and practical performance, the Matern kernel is preferred to the novel NNGP in practical applications.

Reinforcement Learning via Gaussian Processes with Neural Network Dual Kernels

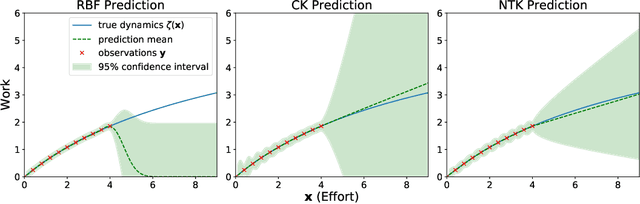
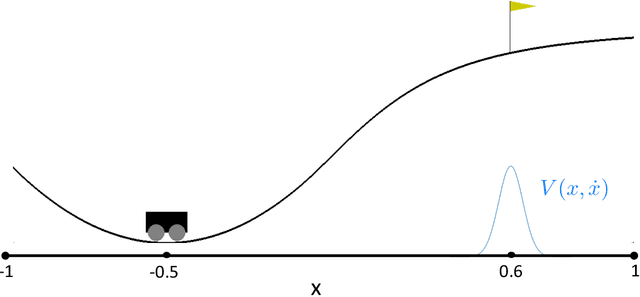
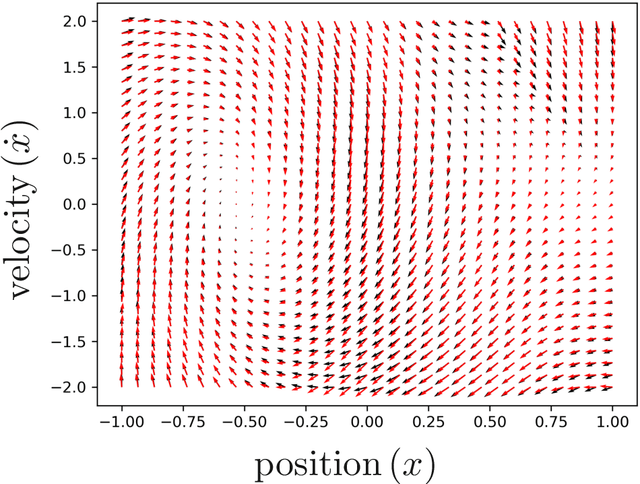
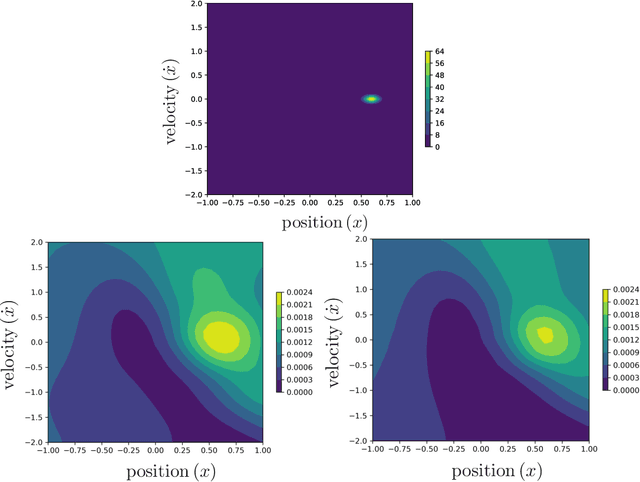
While deep neural networks (DNNs) and Gaussian Processes (GPs) are both popularly utilized to solve problems in reinforcement learning, both approaches feature undesirable drawbacks for challenging problems. DNNs learn complex nonlinear embeddings, but do not naturally quantify uncertainty and are often data-inefficient to train. GPs infer posterior distributions over functions, but popular kernels exhibit limited expressivity on complex and high-dimensional data. Fortunately, recently discovered conjugate and neural tangent kernel functions encode the behavior of overparameterized neural networks in the kernel domain. We demonstrate that these kernels can be efficiently applied to regression and reinforcement learning problems by analyzing a baseline case study. We apply GPs with neural network dual kernels to solve reinforcement learning tasks for the first time. We demonstrate, using the well-understood mountain-car problem, that GPs empowered with dual kernels perform at least as well as those using the conventional radial basis function kernel. We conjecture that by inheriting the probabilistic rigor of GPs and the powerful embedding properties of DNNs, GPs using NN dual kernels will empower future reinforcement learning models on difficult domains.