Dynamics of spherical telescopic linear driven rotation robots

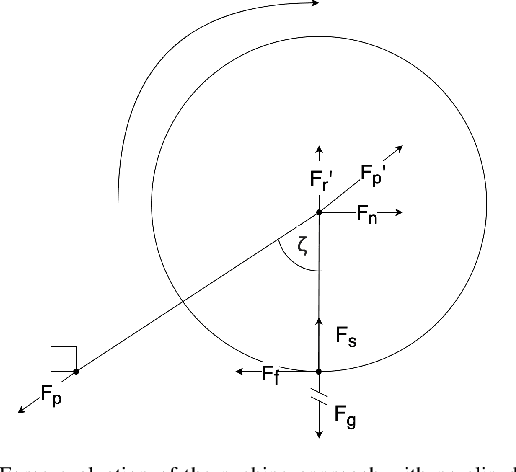
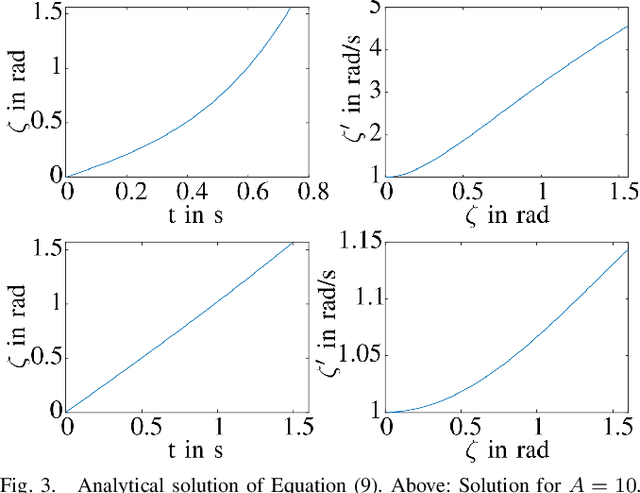
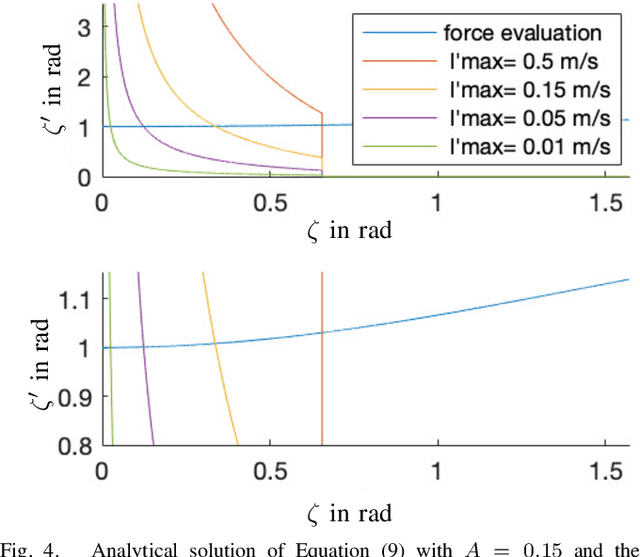
Lunar caves are promising features for long-term and permanent human presence on the moon. However, given their inaccessibility to imaging from survey satellites, the concrete environment within the underground cavities is not well known. Thus, to further the efforts of human presence on the moon, these caves are to be explored by robotic systems. However, a set of environmental factors make this exploration particularly challenging. Among those are the very fine lunar dust that damages exposed sensors and actuators and the unknown composition of the surface and obstacles within the cavity. One robotic system that is particularly fit to meet these challenges is that of a spherical robot, as the exterior shell completely separates the sensors and actuators from the hazardous environment. This work introduces the mathematical description in the form of a dynamic model of a novel locomotion approach for this form factor that adds additional functionality. A set of telescopic linearly extending rods moves the robot using a combination of pushing away from the ground and leveraging the gravitational torque. The approach allows the system to locomote, overcome objects by hoisting its center of gravity on top, and transform into a terrestrial laser scanner by using the rods as a tripod.

Trajectory Optimization and Following for a Three Degrees of Freedom Overactuated Floating Platform

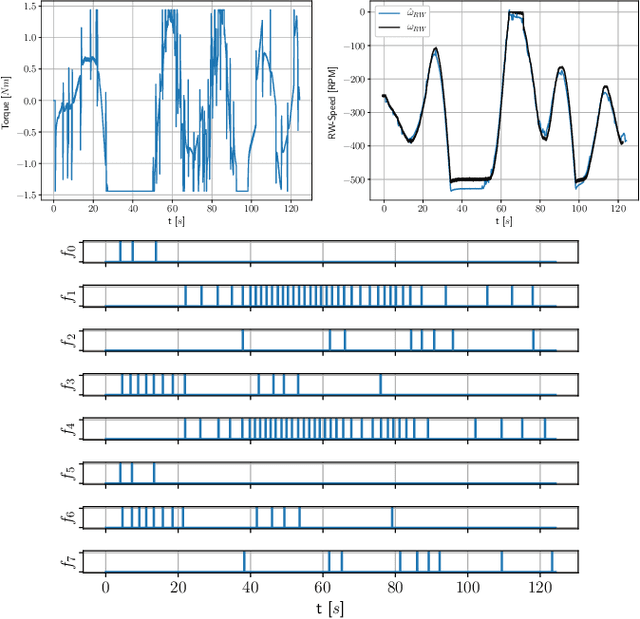
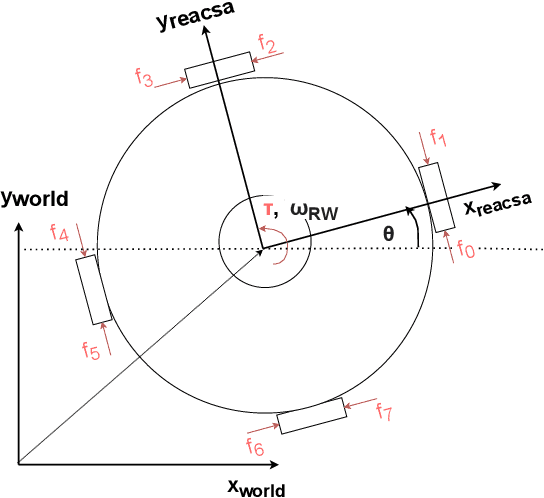
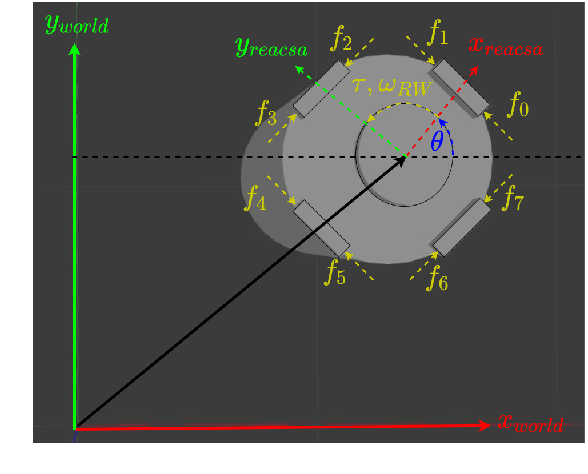
Space robotics applications, such as Active Space Debris Removal (ASDR), require representative testing before launch. A commonly used approach to emulate the microgravity environment in space is air-bearing based platforms on flat-floors, such as the European Space Agency's Orbital Robotics and GNC Lab (ORGL). This work proposes a control architecture for a floating platform at the ORGL, equipped with eight solenoid-valve-based thrusters and one reaction wheel. The control architecture consists of two main components: a trajectory planner that finds optimal trajectories connecting two states and a trajectory follower that follows any physically feasible trajectory. The controller is first evaluated within an introduced simulation, achieving a 100 % success rate at finding and following trajectories to the origin within a Monte-Carlo test. Individual trajectories are also successfully followed by the physical system. In this work, we showcase the ability of the controller to reject disturbances and follow a straight-line trajectory within tens of centimeters.

Finding and Following Optimal Trajectories for an Overactuated Floating Robotic Platform

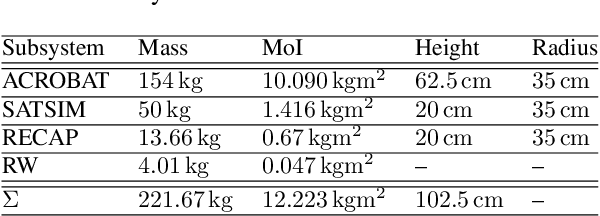
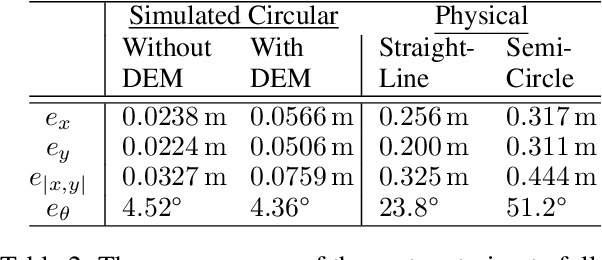
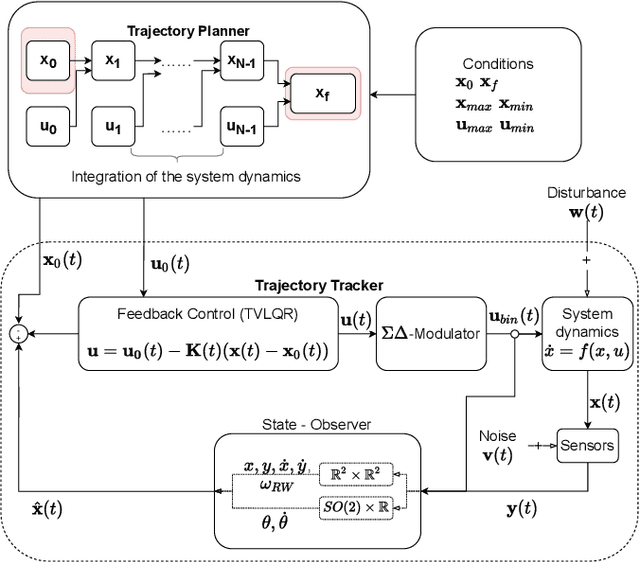
The recent increase in yearly spacecraft launches and the high number of planned launches have raised questions about maintaining accessibility to space for all interested parties. A key to sustaining the future of space-flight is the ability to service malfunctioning - and actively remove dysfunctional spacecraft from orbit. Robotic platforms that autonomously perform these tasks are a topic of ongoing research and thus must undergo thorough testing before launch. For representative system-level testing, the European Space Agency (ESA) uses, among other things, the Orbital Robotics and GNC Lab (ORGL), a flat-floor facility where air-bearing based platforms exhibit free-floating behavior in three Degrees of Freedom (DoF). This work introduces a representative simulation of a free-floating platform in the testing environment and a software framework for controller development. Finally, this work proposes a controller within that framework for finding and following optimal trajectories between arbitrary states, which is evaluated in simulation and reality.

Non-iterative One-step Solution for Point Set Registration Problem on Pose Estimation without Correspondence

In this work, we propose to directly find the one-step solution for the point set registration problem without correspondences. Inspired by the Kernel Correlation method, we consider the full connected objective function between two point sets, thus avoiding the computation of correspondences. By utilizing least square minimization the transformed objective function is directly solved with existing well-known closed-form solutions, e.g., singular value decomposition, that is usually used for given correspondences. However, using equal weights of costs for each connection will degenerate the solution due to the large influence of distant pairs. Thus, we additionally set a scale on each term to avoid the high cost on non-important pairs. As in feature-based registration methods, the similarity between descriptors of points determines the scaling weight. Given the weights we yield a one step solution. As the runtime is in $\mathcal O (n^2)$, we also propose a variant with keypoints that strongly reduce the cost. The experiments show, that our proposed method gives a one-step solution without an initial guess. Our method exhibits competitive outliers robustness, accuracy compared with various methods. And it is more stable to large rotation. In addition, though feature based algorithms are more sensitive to noise, Our method still provide better result compared with the feature match initialized ICP.