Trajectory Optimization and Following for a Three Degrees of Freedom Overactuated Floating Platform

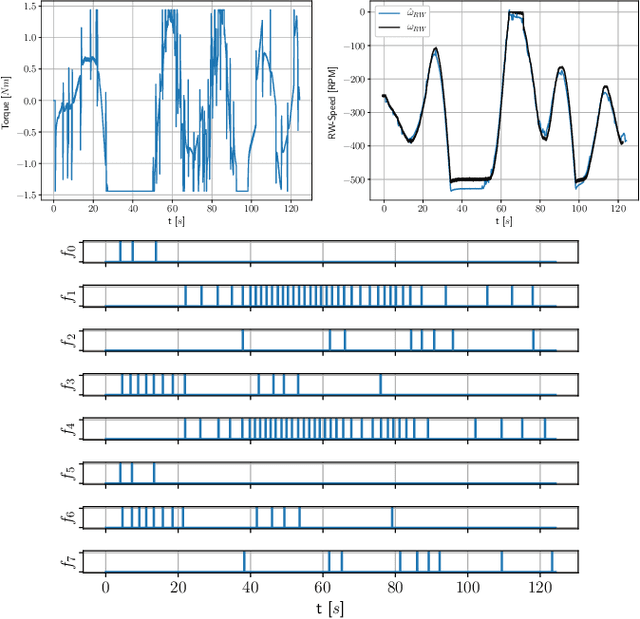
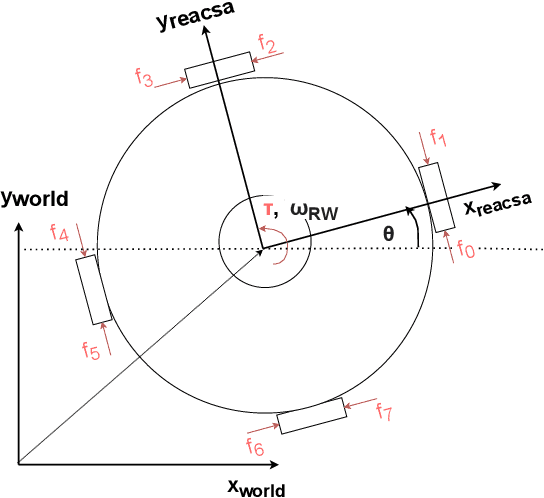
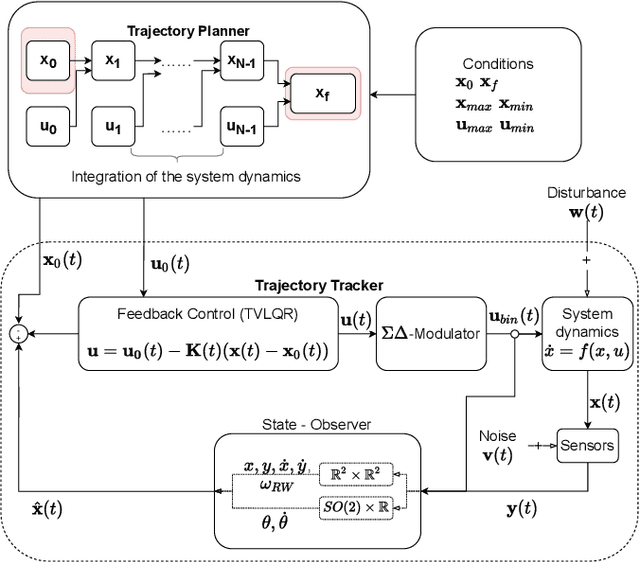
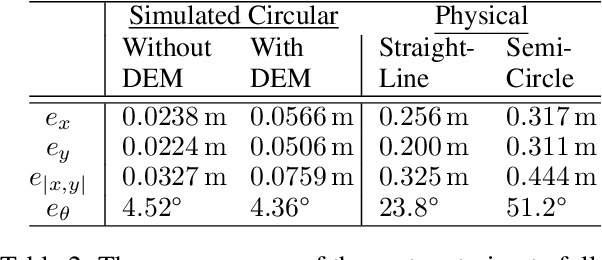
Space robotics applications, such as Active Space Debris Removal (ASDR), require representative testing before launch. A commonly used approach to emulate the microgravity environment in space is air-bearing based platforms on flat-floors, such as the European Space Agency's Orbital Robotics and GNC Lab (ORGL). This work proposes a control architecture for a floating platform at the ORGL, equipped with eight solenoid-valve-based thrusters and one reaction wheel. The control architecture consists of two main components: a trajectory planner that finds optimal trajectories connecting two states and a trajectory follower that follows any physically feasible trajectory. The controller is first evaluated within an introduced simulation, achieving a 100 % success rate at finding and following trajectories to the origin within a Monte-Carlo test. Individual trajectories are also successfully followed by the physical system. In this work, we showcase the ability of the controller to reject disturbances and follow a straight-line trajectory within tens of centimeters.

Finding and Following Optimal Trajectories for an Overactuated Floating Robotic Platform

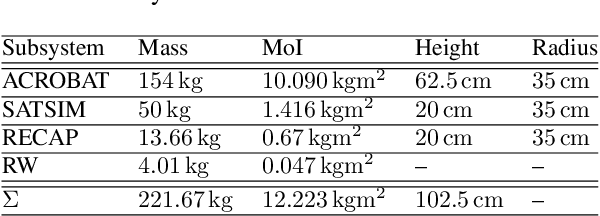
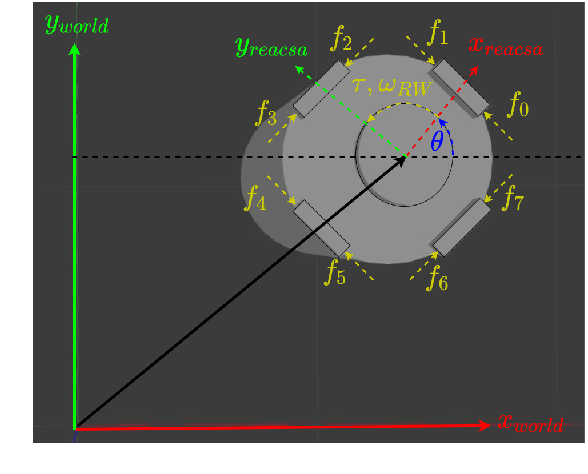
The recent increase in yearly spacecraft launches and the high number of planned launches have raised questions about maintaining accessibility to space for all interested parties. A key to sustaining the future of space-flight is the ability to service malfunctioning - and actively remove dysfunctional spacecraft from orbit. Robotic platforms that autonomously perform these tasks are a topic of ongoing research and thus must undergo thorough testing before launch. For representative system-level testing, the European Space Agency (ESA) uses, among other things, the Orbital Robotics and GNC Lab (ORGL), a flat-floor facility where air-bearing based platforms exhibit free-floating behavior in three Degrees of Freedom (DoF). This work introduces a representative simulation of a free-floating platform in the testing environment and a software framework for controller development. Finally, this work proposes a controller within that framework for finding and following optimal trajectories between arbitrary states, which is evaluated in simulation and reality.