Unicorn: Unified Neural Image Compression with One Number Reconstruction

Prevalent lossy image compression schemes can be divided into: 1) explicit image compression (EIC), including traditional standards and neural end-to-end algorithms; 2) implicit image compression (IIC) based on implicit neural representations (INR). The former is encountering impasses of either leveling off bitrate reduction at a cost of tremendous complexity while the latter suffers from excessive smoothing quality as well as lengthy decoder models. In this paper, we propose an innovative paradigm, which we dub \textbf{Unicorn} (\textbf{U}nified \textbf{N}eural \textbf{I}mage \textbf{C}ompression with \textbf{O}ne \textbf{N}number \textbf{R}econstruction). By conceptualizing the images as index-image pairs and learning the inherent distribution of pairs in a subtle neural network model, Unicorn can reconstruct a visually pleasing image from a randomly generated noise with only one index number. The neural model serves as the unified decoder of images while the noises and indexes corresponds to explicit representations. As a proof of concept, we propose an effective and efficient prototype of Unicorn based on latent diffusion models with tailored model designs. Quantitive and qualitative experimental results demonstrate that our prototype achieves significant bitrates reduction compared with EIC and IIC algorithms. More impressively, benefitting from the unified decoder, our compression ratio escalates as the quantity of images increases. We envision that more advanced model designs will endow Unicorn with greater potential in image compression. We will release our codes in \url{https://github.com/uniqzheng/Unicorn-Laduree}.

Predicting the Output Structure of Sparse Matrix Multiplication with Sampled Compression Ratio

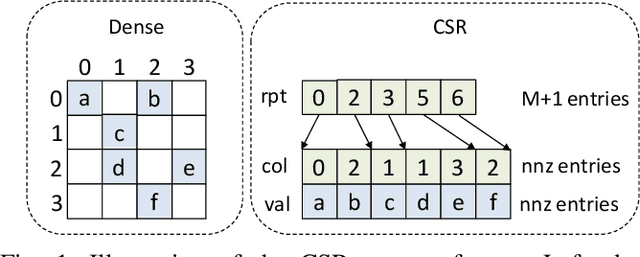
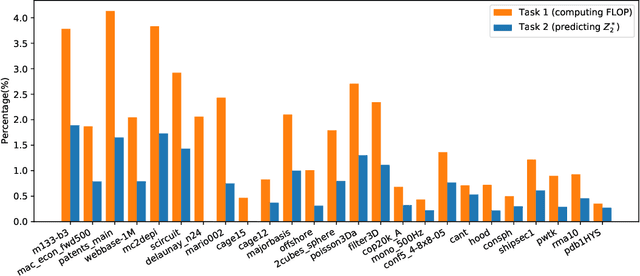
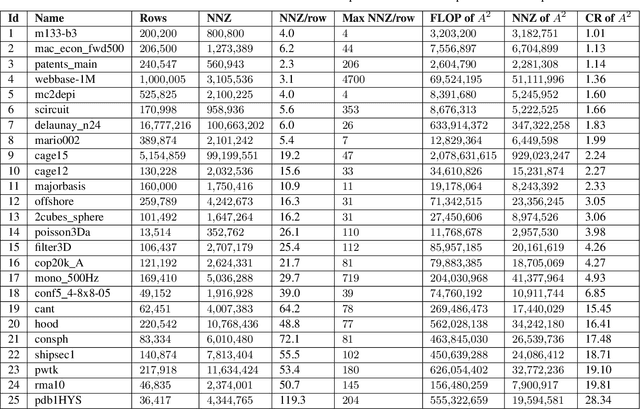
Sparse general matrix multiplication (SpGEMM) is a fundamental building block in numerous scientific applications. One critical task of SpGEMM is to compute or predict the structure of the output matrix (i.e., the number of nonzero elements per output row) for efficient memory allocation and load balance, which impact the overall performance of SpGEMM. Existing work either precisely calculates the output structure or adopts upper-bound or sampling-based methods to predict the output structure. However, these methods either take much execution time or are not accurate enough. In this paper, we propose a novel sampling-based method with better accuracy and low costs compared to the existing sampling-based method. The proposed method first predicts the compression ratio of SpGEMM by leveraging the number of intermediate products (denoted as FLOP) and the number of nonzero elements (denoted as NNZ) of the same sampled result matrix. And then, the predicted output structure is obtained by dividing the FLOP per output row by the predicted compression ratio. We also propose a reference design of the existing sampling-based method with optimized computing overheads to demonstrate the better accuracy of the proposed method. We construct 625 test cases with various matrix dimensions and sparse structures to evaluate the prediction accuracy. Experimental results show that the absolute relative errors of the proposed method and the reference design are 1.56\% and 8.12\%, respectively, on average, and 25\% and 156\%, respectively, in the worst case.