Predicting the Output Structure of Sparse Matrix Multiplication with Sampled Compression Ratio
Paper and Code
Jul 28, 2022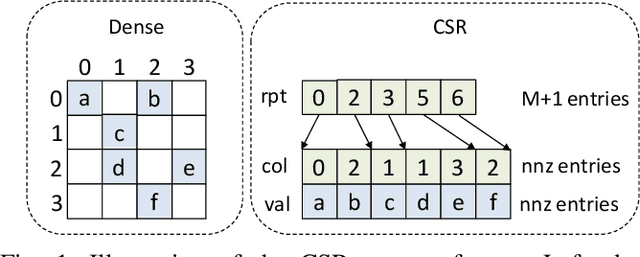
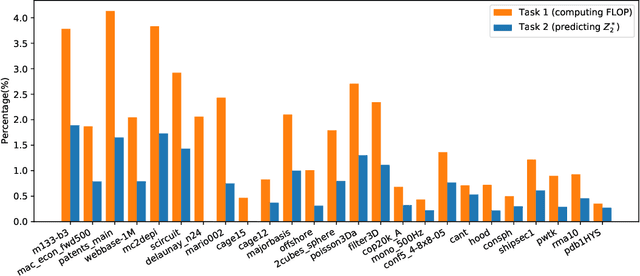
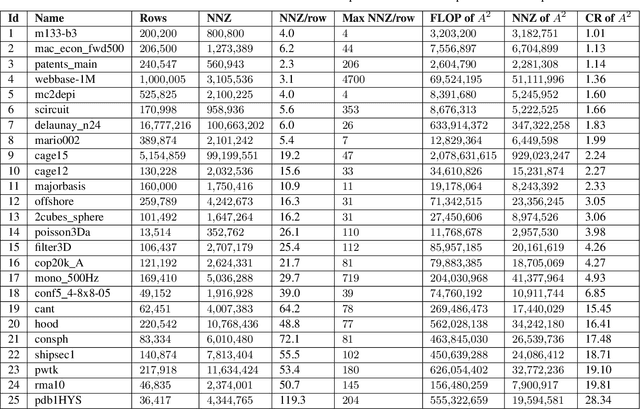
Sparse general matrix multiplication (SpGEMM) is a fundamental building block in numerous scientific applications. One critical task of SpGEMM is to compute or predict the structure of the output matrix (i.e., the number of nonzero elements per output row) for efficient memory allocation and load balance, which impact the overall performance of SpGEMM. Existing work either precisely calculates the output structure or adopts upper-bound or sampling-based methods to predict the output structure. However, these methods either take much execution time or are not accurate enough. In this paper, we propose a novel sampling-based method with better accuracy and low costs compared to the existing sampling-based method. The proposed method first predicts the compression ratio of SpGEMM by leveraging the number of intermediate products (denoted as FLOP) and the number of nonzero elements (denoted as NNZ) of the same sampled result matrix. And then, the predicted output structure is obtained by dividing the FLOP per output row by the predicted compression ratio. We also propose a reference design of the existing sampling-based method with optimized computing overheads to demonstrate the better accuracy of the proposed method. We construct 625 test cases with various matrix dimensions and sparse structures to evaluate the prediction accuracy. Experimental results show that the absolute relative errors of the proposed method and the reference design are 1.56\% and 8.12\%, respectively, on average, and 25\% and 156\%, respectively, in the worst case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge