Dynamic Global Sensitivity for Differentially Private Contextual Bandits

Bandit algorithms have become a reference solution for interactive recommendation. However, as such algorithms directly interact with users for improved recommendations, serious privacy concerns have been raised regarding its practical use. In this work, we propose a differentially private linear contextual bandit algorithm, via a tree-based mechanism to add Laplace or Gaussian noise to model parameters. Our key insight is that as the model converges during online update, the global sensitivity of its parameters shrinks over time (thus named dynamic global sensitivity). Compared with existing solutions, our dynamic global sensitivity analysis allows us to inject less noise to obtain $(\epsilon, \delta)$-differential privacy with added regret caused by noise injection in $\tilde O(\log{T}\sqrt{T}/\epsilon)$. We provide a rigorous theoretical analysis over the amount of noise added via dynamic global sensitivity and the corresponding upper regret bound of our proposed algorithm. Experimental results on both synthetic and real-world datasets confirmed the algorithm's advantage against existing solutions.

Calibrated Predictive Distributions via Diagnostics for Conditional Coverage

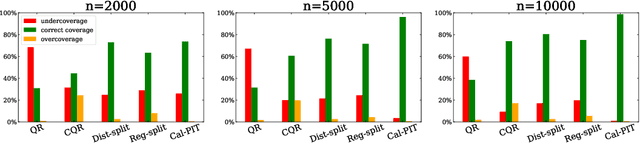
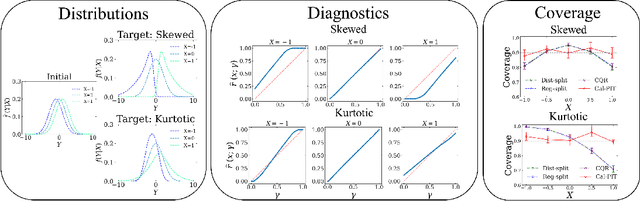
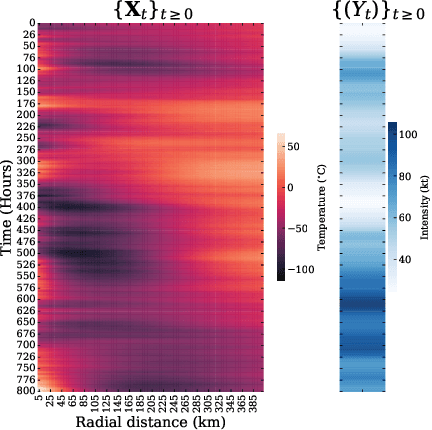
Uncertainty quantification is crucial for assessing the predictive ability of AI algorithms. A large body of work (including normalizing flows and Bayesian neural networks) has been devoted to describing the entire predictive distribution (PD) of a target variable Y given input features $\mathbf{X}$. However, off-the-shelf PDs are usually far from being conditionally calibrated; i.e., the probability of occurrence of an event given input $\mathbf{X}$ can be significantly different from the predicted probability. Most current research on predictive inference (such as conformal prediction) concerns constructing prediction sets, that do not only provide correct uncertainties on average over the entire population (that is, averaging over $\mathbf{X}$), but that are also approximately conditionally calibrated with accurate uncertainties for individual instances. It is often believed that the problem of obtaining and assessing entire conditionally calibrated PDs is too challenging to approach. In this work, we show that recalibration as well as validation are indeed attainable goals in practice. Our proposed method relies on the idea of regressing probability integral transform (PIT) scores against $\mathbf{X}$. This regression gives full diagnostics of conditional coverage across the entire feature space and can be used to recalibrate misspecified PDs. We benchmark our corrected prediction bands against oracle bands and state-of-the-art predictive inference algorithms for synthetic data, including settings with distributional shift and dependent high-dimensional sequence data. Finally, we demonstrate an application to the physical sciences in which we assess and produce calibrated PDs for measurements of galaxy distances using imaging data (i.e., photometric redshifts).

Likelihood-Free Frequentist Inference: Bridging Classical Statistics and Machine Learning in Simulation and Uncertainty Quantification

Many areas of science make extensive use of computer simulators that implicitly encode likelihood functions of complex systems. Classical statistical methods are poorly suited for these so-called likelihood-free inference (LFI) settings, outside the asymptotic and low-dimensional regimes. Although new machine learning methods, such as normalizing flows, have revolutionized the sample efficiency and capacity of LFI methods, it remains an open question whether they produce reliable measures of uncertainty. This paper presents a statistical framework for LFI that unifies classical statistics with modern machine learning to: (1) efficiently construct frequentist confidence sets and hypothesis tests with finite-sample guarantees of nominal coverage (type I error control) and power; (2) provide practical diagnostics for assessing empirical coverage over the entire parameter space. We refer to our framework as likelihood-free frequentist inference (LF2I). Any method that estimates a test statistic, like the likelihood ratio, can be plugged into our framework to create valid confidence sets and compute diagnostics, without costly Monte Carlo samples at fixed parameter settings. In this work, we specifically study the power of two test statistics (ACORE and BFF), which, respectively, maximize versus integrate an odds function over the parameter space. Our study offers multifaceted perspectives on the challenges in LF2I.

MD-split+: Practical Local Conformal Inference in High Dimensions

Quantifying uncertainty in model predictions is a common goal for practitioners seeking more than just point predictions. One tool for uncertainty quantification that requires minimal assumptions is conformal inference, which can help create probabilistically valid prediction regions for black box models. Classical conformal prediction only provides marginal validity, whereas in many situations locally valid prediction regions are desirable. Deciding how best to partition the feature space X when applying localized conformal prediction is still an open question. We present MD-split+, a practical local conformal approach that creates X partitions based on localized model performance of conditional density estimation models. Our method handles complex real-world data settings where such models may be misspecified, and scales to high-dimensional inputs. We discuss how our local partitions philosophically align with expected behavior from an unattainable conditional conformal inference approach. We also empirically compare our method against other local conformal approaches.

Reinforcement learning for bandwidth estimation and congestion control in real-time communications

Bandwidth estimation and congestion control for real-time communications (i.e., audio and video conferencing) remains a difficult problem, despite many years of research. Achieving high quality of experience (QoE) for end users requires continual updates due to changing network architectures and technologies. In this paper, we apply reinforcement learning for the first time to the problem of real-time communications (RTC), where we seek to optimize user-perceived quality. We present initial proof-of-concept results, where we learn an agent to control sending rate in an RTC system, evaluating using both network simulation and real Internet video calls. We discuss the challenges we observed, particularly in designing realistic reward functions that reflect QoE, and in bridging the gap between the training environment and real-world networks.

Cryptocurrency Price Prediction and Trading Strategies Using Support Vector Machines

Few assets in financial history have been as notoriously volatile as cryptocurrencies. While the long term outlook for this asset class remains unclear, we are successful in making short term price predictions for several major crypto assets. Using historical data from July 2015 to November 2019, we develop a large number of technical indicators to capture patterns in the cryptocurrency market. We then test various classification methods to forecast short-term future price movements based on these indicators. On both PPV and NPV metrics, our classifiers do well in identifying up and down market moves over the next 1 hour. Beyond evaluating classification accuracy, we also develop a strategy for translating 1-hour-ahead class predictions into trading decisions, along with a backtester that simulates trading in a realistic environment. We find that support vector machines yield the most profitable trading strategies, which outperform the market on average for Bitcoin, Ethereum and Litecoin over the past 22 months, since January 2018.