Local primordial non-Gaussianity from the large-scale clustering of photometric DESI luminous red galaxies

We use angular clustering of luminous red galaxies from the Dark Energy Spectroscopic Instrument (DESI) imaging surveys to constrain the local primordial non-Gaussianity parameter fNL. Our sample comprises over 12 million targets, covering 14,000 square degrees of the sky, with redshifts in the range 0.2< z < 1.35. We identify Galactic extinction, survey depth, and astronomical seeing as the primary sources of systematic error, and employ linear regression and artificial neural networks to alleviate non-cosmological excess clustering on large scales. Our methods are tested against log-normal simulations with and without fNL and systematics, showing superior performance of the neural network treatment in reducing remaining systematics. Assuming the universality relation, we find fNL $= 47^{+14(+29)}_{-11(-22)}$ at 68\%(95\%) confidence. With a more aggressive treatment, including regression against the full set of imaging maps, our maximum likelihood value shifts slightly to fNL$ \sim 50$ and the uncertainty on fNL increases due to the removal of large-scale clustering information. We apply a series of robustness tests (e.g., cuts on imaging, declination, or scales used) that show consistency in the obtained constraints. Despite extensive efforts to mitigate systematics, our measurements indicate fNL > 0 with a 99.9 percent confidence level. This outcome raises concerns as it could be attributed to unforeseen systematics, including calibration errors or uncertainties associated with low-\ell systematics in the extinction template. Alternatively, it could suggest a scale-dependent fNL model--causing significant non-Gaussianity around large-scale structure while leaving cosmic microwave background scales unaffected. Our results encourage further studies of fNL with DESI spectroscopic samples, where the inclusion of 3D clustering modes should help separate imaging systematics.

Calibrated Predictive Distributions via Diagnostics for Conditional Coverage

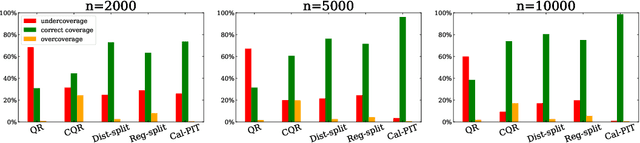
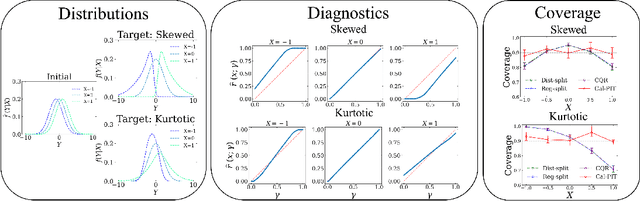
Uncertainty quantification is crucial for assessing the predictive ability of AI algorithms. A large body of work (including normalizing flows and Bayesian neural networks) has been devoted to describing the entire predictive distribution (PD) of a target variable Y given input features $\mathbf{X}$. However, off-the-shelf PDs are usually far from being conditionally calibrated; i.e., the probability of occurrence of an event given input $\mathbf{X}$ can be significantly different from the predicted probability. Most current research on predictive inference (such as conformal prediction) concerns constructing prediction sets, that do not only provide correct uncertainties on average over the entire population (that is, averaging over $\mathbf{X}$), but that are also approximately conditionally calibrated with accurate uncertainties for individual instances. It is often believed that the problem of obtaining and assessing entire conditionally calibrated PDs is too challenging to approach. In this work, we show that recalibration as well as validation are indeed attainable goals in practice. Our proposed method relies on the idea of regressing probability integral transform (PIT) scores against $\mathbf{X}$. This regression gives full diagnostics of conditional coverage across the entire feature space and can be used to recalibrate misspecified PDs. We benchmark our corrected prediction bands against oracle bands and state-of-the-art predictive inference algorithms for synthetic data, including settings with distributional shift and dependent high-dimensional sequence data. Finally, we demonstrate an application to the physical sciences in which we assess and produce calibrated PDs for measurements of galaxy distances using imaging data (i.e., photometric redshifts).