SCASRec: A Self-Correcting and Auto-Stopping Model for Generative Route List Recommendation

Route recommendation systems commonly adopt a multi-stage pipeline involving fine-ranking and re-ranking to produce high-quality ordered recommendations. However, this paradigm faces three critical limitations. First, there is a misalignment between offline training objectives and online metrics. Offline gains do not necessarily translate to online improvements. Actual performance must be validated through A/B testing, which may potentially compromise the user experience. Second, redundancy elimination relies on rigid, handcrafted rules that lack adaptability to the high variance in user intent and the unstructured complexity of real-world scenarios. Third, the strict separation between fine-ranking and re-ranking stages leads to sub-optimal performance. Since each module is optimized in isolation, the fine-ranking stage remains oblivious to the list-level objectives (e.g., diversity) targeted by the re-ranker, thereby preventing the system from achieving a jointly optimized global optimum. To overcome these intertwined challenges, we propose \textbf{SCASRec} (\textbf{S}elf-\textbf{C}orrecting and \textbf{A}uto-\textbf{S}topping \textbf{Rec}ommendation), a unified generative framework that integrates ranking and redundancy elimination into a single end-to-end process. SCASRec introduces a stepwise corrective reward (SCR) to guide list-wise refinement by focusing on hard samples, and employs a learnable End-of-Recommendation (EOR) token to terminate generation adaptively when no further improvement is expected. Experiments on two large-scale, open-sourced route recommendation datasets demonstrate that SCASRec establishes an SOTA in offline and online settings. SCASRec has been fully deployed in a real-world navigation app, demonstrating its effectiveness.

DOGMA: Weaving Structural Information into Data-centric Single-cell Transcriptomics Analysis

Recently, data-centric AI methodology has been a dominant paradigm in single-cell transcriptomics analysis, which treats data representation rather than model complexity as the fundamental bottleneck. In the review of current studies, earlier sequence methods treat cells as independent entities and adapt prevalent ML models to analyze their directly inherited sequence data. Despite their simplicity and intuition, these methods overlook the latent intercellular relationships driven by the functional mechanisms of biological systems and the inherent quality issues of the raw sequence data. Therefore, a series of structured methods has emerged. Although they employ various heuristic rules to capture intricate intercellular relationships and enhance the raw sequencing data, these methods often neglect biological prior knowledge. This omission incurs substantial overhead and yields suboptimal graph representations, thereby hindering the utility of ML models. To address them, we propose DOGMA, a holistic data-centric framework designed for the structural reshaping and semantic enhancement of raw data through multi-level biological prior knowledge. Transcending reliance on stochastic heuristics, DOGMA redefines graph construction by integrating Statistical Anchors with Cell Ontology and Phylogenetic Trees to enable deterministic structure discovery and robust cross-species alignment. Furthermore, Gene Ontology is utilized to bridge the feature-level semantic gap by incorporating functional priors. In complex multi-species and multi-organ benchmarks, DOGMA achieves SOTA performance, exhibiting superior zero-shot robustness and sample efficiency while operating with significantly lower computational cost.

LION: A Clifford Neural Paradigm for Multimodal-Attributed Graph Learning

Recently, the rapid advancement of multimodal domains has driven a data-centric paradigm shift in graph ML, transitioning from text-attributed to multimodal-attributed graphs. This advancement significantly enhances data representation and expands the scope of graph downstream tasks, such as modality-oriented tasks, thereby improving the practical utility of graph ML. Despite its promise, limitations exist in the current neural paradigms: (1) Neglect Context in Modality Alignment: Most existing methods adopt topology-constrained or modality-specific operators as tokenizers. These aligners inevitably neglect graph context and inhibit modality interaction, resulting in suboptimal alignment. (2) Lack of Adaptation in Modality Fusion: Most existing methods are simple adaptations for 2-modality graphs and fail to adequately exploit aligned tokens equipped with topology priors during fusion, leading to poor generalizability and performance degradation. To address the above issues, we propose LION (c\underline{LI}ff\underline{O}rd \underline{N}eural paradigm) based on the Clifford algebra and decoupled graph neural paradigm (i.e., propagation-then-aggregation) to implement alignment-then-fusion in multimodal-attributed graphs. Specifically, we first construct a modality-aware geometric manifold grounded in Clifford algebra. This geometric-induced high-order graph propagation efficiently achieves modality interaction, facilitating modality alignment. Then, based on the geometric grade properties of aligned tokens, we propose adaptive holographic aggregation. This module integrates the energy and scale of geometric grades with learnable parameters to improve modality fusion. Extensive experiments on 9 datasets demonstrate that LION significantly outperforms SOTA baselines across 3 graph and 3 modality downstream tasks.

Two Sides of the Same Optimization Coin: Model Degradation and Representation Collapse in Graph Foundation Models

Graph foundation models, inspired by the success of LLMs, are designed to learn the optimal embedding from multi-domain TAGs for the downstream cross-task generalization capability. During our investigation, graph VQ-MAE stands out among the increasingly diverse landscape of GFM architectures. This is attributed to its ability to jointly encode topology and textual attributes from multiple domains into discrete embedding spaces with clear semantic boundaries. Despite its potential, domain generalization conflicts cause imperceptible pitfalls. In this paper, we instantiate two of them, and they are just like two sides of the same GFM optimization coin - Side 1 Model Degradation: The encoder and codebook fail to capture the diversity of inputs; Side 2 Representation Collapse: The hidden embedding and codebook vector fail to preserve semantic separability due to constraints from narrow representation subspaces. These two pitfalls (sides) collectively impair the decoder and generate the low-quality reconstructed supervision, causing the GFM optimization dilemma during pre-training (coin). Through empirical investigation, we attribute the above challenges to Information Bottleneck and Regularization Deficit. To address them, we propose MoT (Mixture-of-Tinkers) - (1) Information Tinker for Two Pitfalls, which utilizes an edge-wise semantic fusion strategy and a mixture-of-codebooks with domain-aware routing to improve information capacity. (2) Regularization Tinker for Optimization Coin, which utilizes two additional regularizations to further improve gradient supervision in our proposed Information Tinker. Notably, as a flexible architecture, MoT adheres to the scaling laws of GFM, offering a controllable model scale. Compared to SOTA baselines, experiments on 22 datasets across 6 domains demonstrate that MoT achieves significant improvements in supervised, few-shot, and zero-shot scenarios.

Towards Unbiased Federated Graph Learning: Label and Topology Perspectives

Federated Graph Learning (FGL) enables privacy-preserving, distributed training of graph neural networks without sharing raw data. Among its approaches, subgraph-FL has become the dominant paradigm, with most work focused on improving overall node classification accuracy. However, these methods often overlook fairness due to the complexity of node features, labels, and graph structures. In particular, they perform poorly on nodes with disadvantaged properties, such as being in the minority class within subgraphs or having heterophilous connections (neighbors with dissimilar labels or misleading features). This reveals a critical issue: high accuracy can mask degraded performance on structurally or semantically marginalized nodes. To address this, we advocate for two fairness goals: (1) improving representation of minority class nodes for class-wise fairness and (2) mitigating topological bias from heterophilous connections for topology-aware fairness. We propose FairFGL, a novel framework that enhances fairness through fine-grained graph mining and collaborative learning. On the client side, the History-Preserving Module prevents overfitting to dominant local classes, while the Majority Alignment Module refines representations of heterophilous majority-class nodes. The Gradient Modification Module transfers minority-class knowledge from structurally favorable clients to improve fairness. On the server side, FairFGL uploads only the most influenced subset of parameters to reduce communication costs and better reflect local distributions. A cluster-based aggregation strategy reconciles conflicting updates and curbs global majority dominance . Extensive evaluations on eight benchmarks show FairFGL significantly improves minority-group performance , achieving up to a 22.62 percent Macro-F1 gain while enhancing convergence over state-of-the-art baselines.

Toward Effective Digraph Representation Learning: A Magnetic Adaptive Propagation based Approach

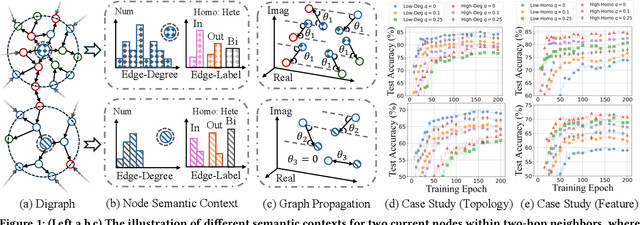
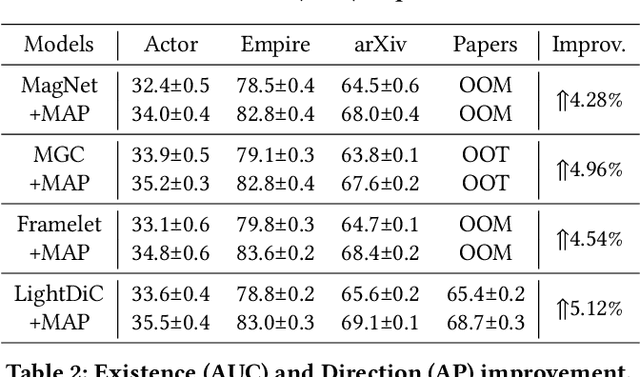
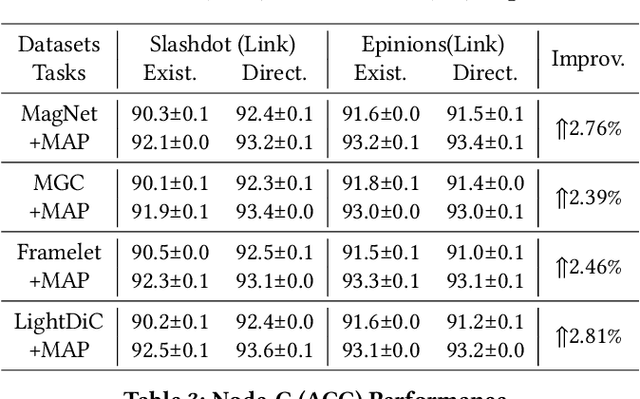
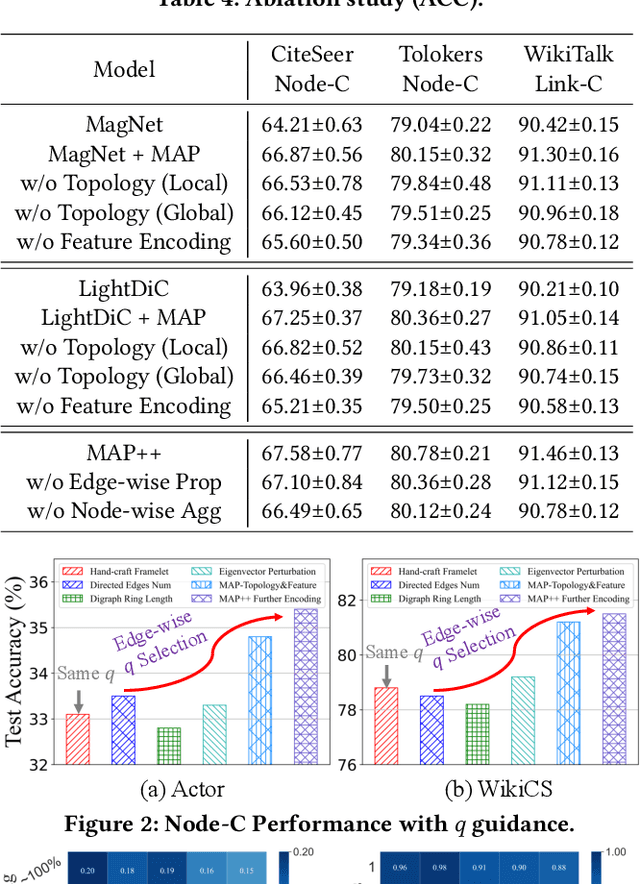
The $q$-parameterized magnetic Laplacian serves as the foundation of directed graph (digraph) convolution, enabling this kind of digraph neural network (MagDG) to encode node features and structural insights by complex-domain message passing. As a generalization of undirected methods, MagDG shows superior capability in modeling intricate web-scale topology. Despite the great success achieved by existing MagDGs, limitations still exist: (1) Hand-crafted $q$: The performance of MagDGs depends on selecting an appropriate $q$-parameter to construct suitable graph propagation equations in the complex domain. This parameter tuning, driven by downstream tasks, limits model flexibility and significantly increases manual effort. (2) Coarse Message Passing: Most approaches treat all nodes with the same complex-domain propagation and aggregation rules, neglecting their unique digraph contexts. This oversight results in sub-optimal performance. To address the above issues, we propose two key techniques: (1) MAP is crafted to be a plug-and-play complex-domain propagation optimization strategy in the context of digraph learning, enabling seamless integration into any MagDG to improve predictions while enjoying high running efficiency. (2) MAP++ is a new digraph learning framework, further incorporating a learnable mechanism to achieve adaptively edge-wise propagation and node-wise aggregation in the complex domain for better performance. Extensive experiments on 12 datasets demonstrate that MAP enjoys flexibility for it can be incorporated with any MagDG, and scalability as it can deal with web-scale digraphs. MAP++ achieves SOTA predictive performance on 4 different downstream tasks.

Towards Data-centric Machine Learning on Directed Graphs: a Survey

In recent years, Graph Neural Networks (GNNs) have made significant advances in processing structured data. However, most of them primarily adopted a model-centric approach, which simplifies graphs by converting it into undirected formats and emphasizes model designs. This approach is inherently constrained in real-world applications due to inevitable information loss in simple undirected graphs and data-driven model optimization dilemmas associated with exceeding the upper bounds of representational capacity. As a result, there has been a shift toward data-centric methods that prioritize improving graph quality and representation. Specifically, various types of graphs can be derived from naturally structured data, including heterogeneous graphs, hypergraphs, and directed graphs. Among these, directed graphs offer distinct advantages in topological systems by modeling causal relationships, and directed GNNs have been extensively studied in recent years. However, a comprehensive survey of this emerging topic is still lacking. Therefore, we aim to provide a comprehensive review of directed graph learning, with a particular focus on a data-centric perspective. Specifically, we first introduce a novel taxonomy for existing studies. Subsequently, we re-examine these methods from the data-centric perspective, with an emphasis on understanding and improving data representation. It demonstrates that a deep understanding of directed graphs and its quality plays a crucial role in model performance. Additionally, we explore the diverse applications of directed GNNs across 10+ domains, highlighting their broad applicability. Finally, we identify key opportunities and challenges within the field, offering insights that can guide future research and development in directed graph learning.

DiRW: Path-Aware Digraph Learning for Heterophily

Recently, graph neural network (GNN) has emerged as a powerful representation learning tool for graph-structured data. However, most approaches are tailored for undirected graphs, neglecting the abundant information embedded in the edges of directed graphs (digraphs). In fact, digraphs are widely applied in the real world (e.g., social networks and recommendations) and are also confirmed to offer a new perspective for addressing topological heterophily challenges (i.e., connected nodes have complex patterns of feature distribution or labels). Despite recent significant advancements in DiGNNs, existing spatial- and spectral-based methods have inherent limitations due to the complex learning mechanisms and reliance on high-quality topology, leading to low efficiency and unstable performance. To address these issues, we propose Directed Random Walk (DiRW), which can be viewed as a plug-and-play strategy or an innovative neural architecture that provides a guidance or new learning paradigm for most spatial-based methods or digraphs. Specifically, DiRW incorporates a direction-aware path sampler optimized from the perspectives of walk probability, length, and number in a weight-free manner by considering node profiles and topological structure. Building upon this, DiRW utilizes a node-wise learnable path aggregator for generalized messages obtained by our proposed adaptive walkers to represent the current node. Extensive experiments on 9 datasets demonstrate that DiRW: (1) enhances most spatial-based methods as a plug-and-play strategy; (2) achieves SOTA performance as a new digraph learning paradigm.

Rethinking Node-wise Propagation for Large-scale Graph Learning

Scalable graph neural networks (GNNs) have emerged as a promising technique, which exhibits superior predictive performance and high running efficiency across numerous large-scale graph-based web applications. However, (i) Most scalable GNNs tend to treat all nodes in graphs with the same propagation rules, neglecting their topological uniqueness; (ii) Existing node-wise propagation optimization strategies are insufficient on web-scale graphs with intricate topology, where a full portrayal of nodes' local properties is required. Intuitively, different nodes in web-scale graphs possess distinct topological roles, and therefore propagating them indiscriminately or neglect local contexts may compromise the quality of node representations. This intricate topology in web-scale graphs cannot be matched by small-scale scenarios. To address the above issues, we propose \textbf{A}daptive \textbf{T}opology-aware \textbf{P}ropagation (ATP), which reduces potential high-bias propagation and extracts structural patterns of each node in a scalable manner to improve running efficiency and predictive performance. Remarkably, ATP is crafted to be a plug-and-play node-wise propagation optimization strategy, allowing for offline execution independent of the graph learning process in a new perspective. Therefore, this approach can be seamlessly integrated into most scalable GNNs while remain orthogonal to existing node-wise propagation optimization strategies. Extensive experiments on 12 datasets, including the most representative large-scale ogbn-papers100M, have demonstrated the effectiveness of ATP. Specifically, ATP has proven to be efficient in improving the performance of prevalent scalable GNNs for semi-supervised node classification while addressing redundant computational costs.

LightDiC: A Simple yet Effective Approach for Large-scale Digraph Representation Learning

Most existing graph neural networks (GNNs) are limited to undirected graphs, whose restricted scope of the captured relational information hinders their expressive capabilities and deployments in real-world scenarios. Compared with undirected graphs, directed graphs (digraphs) fit the demand for modeling more complex topological systems by capturing more intricate relationships between nodes, such as formulating transportation and financial networks. While some directed GNNs have been introduced, their inspiration mainly comes from deep learning architectures, which lead to redundant complexity and computation, making them inapplicable to large-scale databases. To address these issues, we propose LightDiC, a scalable variant of the digraph convolution based on the magnetic Laplacian. Since topology-related computations are conducted solely during offline pre-processing, LightDiC achieves exceptional scalability, enabling downstream predictions to be trained separately without incurring recursive computational costs. Theoretical analysis shows that LightDiC utilizes directed information to achieve message passing based on the complex field, which corresponds to the proximal gradient descent process of the Dirichlet energy optimization function from the perspective of digraph signal denoising, ensuring its expressiveness. Experimental results demonstrate that LightDiC performs comparably well or even outperforms other SOTA methods in various downstream tasks, with fewer learnable parameters and higher training efficiency. Notably, LightDiC is the first DiGNN to provide satisfactory results in the most representative large-scale database (ogbn-papers100M).