Efficient Exact Resistance Distance Computation on Small-Treewidth Graphs: a Labelling Approach

Resistance distance computation is a fundamental problem in graph analysis, yet existing random walk-based methods are limited to approximate solutions and suffer from poor efficiency on small-treewidth graphs (e.g., road networks). In contrast, shortest-path distance computation achieves remarkable efficiency on such graphs by leveraging cut properties and tree decompositions. Motivated by this disparity, we first analyze the cut property of resistance distance. While a direct generalization proves impractical due to costly matrix operations, we overcome this limitation by integrating tree decompositions, revealing that the resistance distance $r(s,t)$ depends only on labels along the paths from $s$ and $t$ to the root of the decomposition. This insight enables compact labelling structures. Based on this, we propose \treeindex, a novel index method that constructs a resistance distance labelling of size $O(n \cdot h_{\mathcal{G}})$ in $O(n \cdot h_{\mathcal{G}}^2 \cdot d_{\max})$ time, where $h_{\mathcal{G}}$ (tree height) and $d_{\max}$ (maximum degree) behave as small constants in many real-world small-treewidth graphs (e.g., road networks). Our labelling supports exact single-pair queries in $O(h_{\mathcal{G}})$ time and single-source queries in $O(n \cdot h_{\mathcal{G}})$ time. Extensive experiments show that TreeIndex substantially outperforms state-of-the-art approaches. For instance, on the full USA road network, it constructs a $405$ GB labelling in $7$ hours (single-threaded) and answers exact single-pair queries in $10^{-3}$ seconds and single-source queries in $190$ seconds--the first exact method scalable to such large graphs.

Scaling Up Graph Propagation Computation on Large Graphs: A Local Chebyshev Approximation Approach

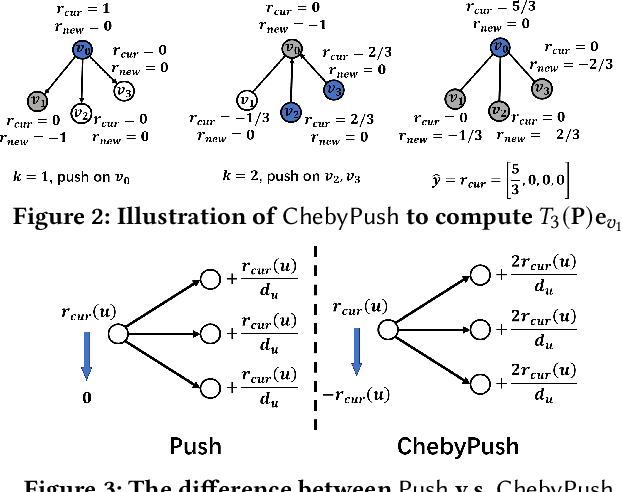
Graph propagation (GP) computation plays a crucial role in graph data analysis, supporting various applications such as graph node similarity queries, graph node ranking, graph clustering, and graph neural networks. Existing methods, mainly relying on power iteration or push computation frameworks, often face challenges with slow convergence rates when applied to large-scale graphs. To address this issue, we propose a novel and powerful approach that accelerates power iteration and push methods using Chebyshev polynomials. Specifically, we first present a novel Chebyshev expansion formula for general GP functions, offering a new perspective on GP computation and achieving accelerated convergence. Building on these theoretical insights, we develop a novel Chebyshev power iteration method (\ltwocheb) and a novel Chebyshev push method (\chebpush). Our \ltwocheb method demonstrates an approximate acceleration of $O(\sqrt{N})$ compared to existing power iteration techniques for both personalized PageRank and heat kernel PageRank computations, which are well-studied GP problems. For \chebpush, we propose an innovative subset Chebyshev recurrence technique, enabling the design of a push-style local algorithm with provable error guarantee and reduced time complexity compared to existing push methods. We conduct extensive experiments using 5 large real-world datasets to evaluate our proposed algorithms, demonstrating their superior efficiency compared to state-of-the-art approaches.

LightDiC: A Simple yet Effective Approach for Large-scale Digraph Representation Learning

Most existing graph neural networks (GNNs) are limited to undirected graphs, whose restricted scope of the captured relational information hinders their expressive capabilities and deployments in real-world scenarios. Compared with undirected graphs, directed graphs (digraphs) fit the demand for modeling more complex topological systems by capturing more intricate relationships between nodes, such as formulating transportation and financial networks. While some directed GNNs have been introduced, their inspiration mainly comes from deep learning architectures, which lead to redundant complexity and computation, making them inapplicable to large-scale databases. To address these issues, we propose LightDiC, a scalable variant of the digraph convolution based on the magnetic Laplacian. Since topology-related computations are conducted solely during offline pre-processing, LightDiC achieves exceptional scalability, enabling downstream predictions to be trained separately without incurring recursive computational costs. Theoretical analysis shows that LightDiC utilizes directed information to achieve message passing based on the complex field, which corresponds to the proximal gradient descent process of the Dirichlet energy optimization function from the perspective of digraph signal denoising, ensuring its expressiveness. Experimental results demonstrate that LightDiC performs comparably well or even outperforms other SOTA methods in various downstream tasks, with fewer learnable parameters and higher training efficiency. Notably, LightDiC is the first DiGNN to provide satisfactory results in the most representative large-scale database (ogbn-papers100M).

Locally Differentially Private Graph Embedding

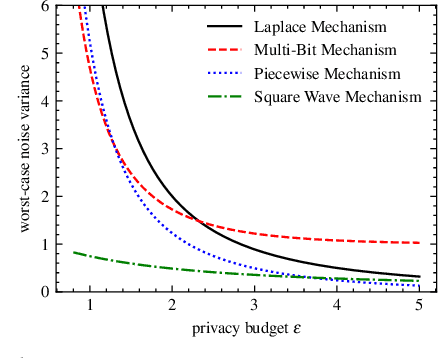
Graph embedding has been demonstrated to be a powerful tool for learning latent representations for nodes in a graph. However, despite its superior performance in various graph-based machine learning tasks, learning over graphs can raise significant privacy concerns when graph data involves sensitive information. To address this, in this paper, we investigate the problem of developing graph embedding algorithms that satisfy local differential privacy (LDP). We propose LDP-GE, a novel privacy-preserving graph embedding framework, to protect the privacy of node data. Specifically, we propose an LDP mechanism to obfuscate node data and adopt personalized PageRank as the proximity measure to learn node representations. Then, we theoretically analyze the privacy guarantees and utility of the LDP-GE framework. Extensive experiments conducted over several real-world graph datasets demonstrate that LDP-GE achieves favorable privacy-utility trade-offs and significantly outperforms existing approaches in both node classification and link prediction tasks.