Scaling Up Graph Propagation Computation on Large Graphs: A Local Chebyshev Approximation Approach

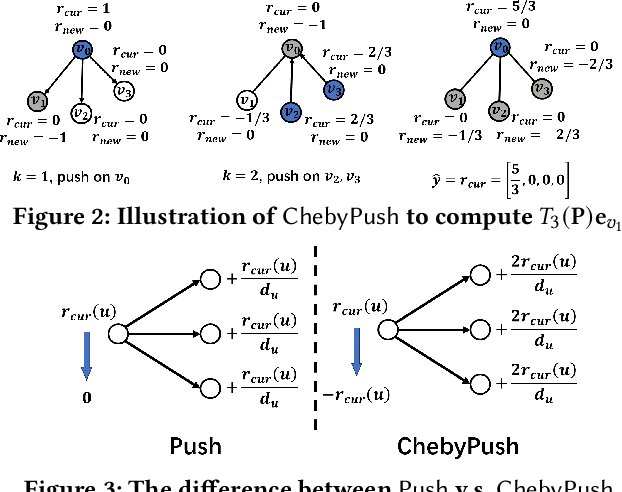
Graph propagation (GP) computation plays a crucial role in graph data analysis, supporting various applications such as graph node similarity queries, graph node ranking, graph clustering, and graph neural networks. Existing methods, mainly relying on power iteration or push computation frameworks, often face challenges with slow convergence rates when applied to large-scale graphs. To address this issue, we propose a novel and powerful approach that accelerates power iteration and push methods using Chebyshev polynomials. Specifically, we first present a novel Chebyshev expansion formula for general GP functions, offering a new perspective on GP computation and achieving accelerated convergence. Building on these theoretical insights, we develop a novel Chebyshev power iteration method (\ltwocheb) and a novel Chebyshev push method (\chebpush). Our \ltwocheb method demonstrates an approximate acceleration of $O(\sqrt{N})$ compared to existing power iteration techniques for both personalized PageRank and heat kernel PageRank computations, which are well-studied GP problems. For \chebpush, we propose an innovative subset Chebyshev recurrence technique, enabling the design of a push-style local algorithm with provable error guarantee and reduced time complexity compared to existing push methods. We conduct extensive experiments using 5 large real-world datasets to evaluate our proposed algorithms, demonstrating their superior efficiency compared to state-of-the-art approaches.

PSNE: Efficient Spectral Sparsification Algorithms for Scaling Network Embedding

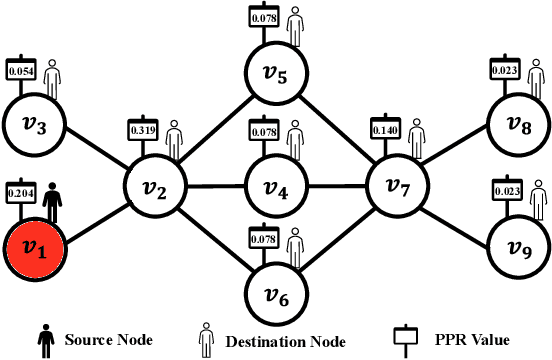
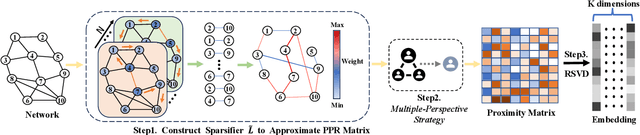
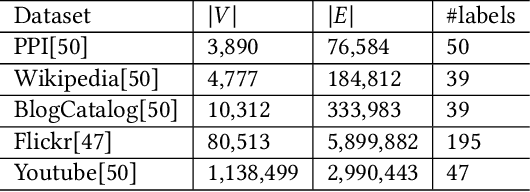
Network embedding has numerous practical applications and has received extensive attention in graph learning, which aims at mapping vertices into a low-dimensional and continuous dense vector space by preserving the underlying structural properties of the graph. Many network embedding methods have been proposed, among which factorization of the Personalized PageRank (PPR for short) matrix has been empirically and theoretically well supported recently. However, several fundamental issues cannot be addressed. (1) Existing methods invoke a seminal Local Push subroutine to approximate \textit{a single} row or column of the PPR matrix. Thus, they have to execute $n$ ($n$ is the number of nodes) Local Push subroutines to obtain a provable PPR matrix, resulting in prohibitively high computational costs for large $n$. (2) The PPR matrix has limited power in capturing the structural similarity between vertices, leading to performance degradation. To overcome these dilemmas, we propose PSNE, an efficient spectral s\textbf{P}arsification method for \textbf{S}caling \textbf{N}etwork \textbf{E}mbedding, which can fast obtain the embedding vectors that retain strong structural similarities. Specifically, PSNE first designs a matrix polynomial sparser to accelerate the calculation of the PPR matrix, which has a theoretical guarantee in terms of the Frobenius norm. Subsequently, PSNE proposes a simple but effective multiple-perspective strategy to enhance further the representation power of the obtained approximate PPR matrix. Finally, PSNE applies a randomized singular value decomposition algorithm on the sparse and multiple-perspective PPR matrix to get the target embedding vectors. Experimental evaluation of real-world and synthetic datasets shows that our solutions are indeed more efficient, effective, and scalable compared with ten competitors.

Scalable and Effective Conductance-based Graph Clustering

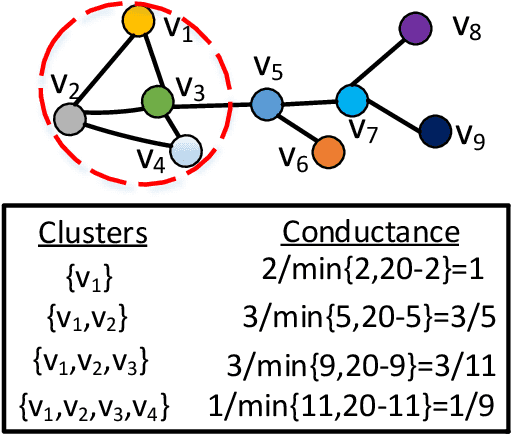
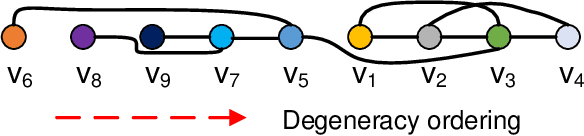
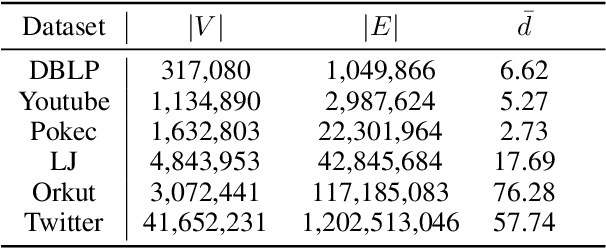
Conductance-based graph clustering has been recognized as a fundamental operator in numerous graph analysis applications. Despite the significant success of conductance-based graph clustering, existing algorithms are either hard to obtain satisfactory clustering qualities, or have high time and space complexity to achieve provable clustering qualities. To overcome these limitations, we devise a powerful \textit{peeling}-based graph clustering framework \textit{PCon}. We show that many existing solutions can be reduced to our framework. Namely, they first define a score function for each vertex, then iteratively remove the vertex with the smallest score. Finally, they output the result with the smallest conductance during the peeling process. Based on our framework, we propose two novel algorithms \textit{PCon\_core} and \emph{PCon\_de} with linear time and space complexity, which can efficiently and effectively identify clusters from massive graphs with more than a few billion edges. Surprisingly, we prove that \emph{PCon\_de} can identify clusters with near-constant approximation ratio, resulting in an important theoretical improvement over the well-known quadratic Cheeger bound. Empirical results on real-life and synthetic datasets show that our algorithms can achieve 5$\sim$42 times speedup with a high clustering accuracy, while using 1.4$\sim$7.8 times less memory than the baseline algorithms.