PSNE: Efficient Spectral Sparsification Algorithms for Scaling Network Embedding
Paper and Code
Aug 05, 2024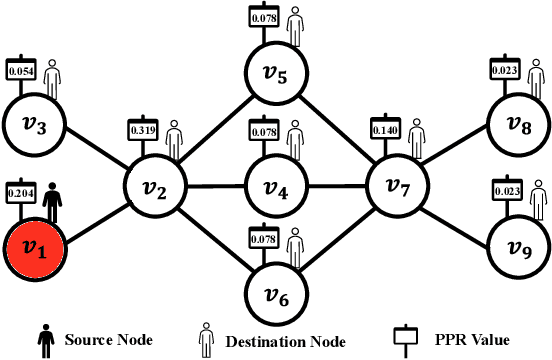

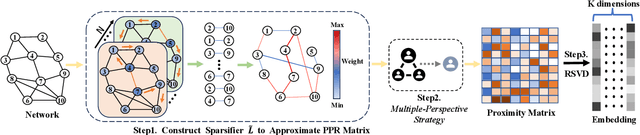
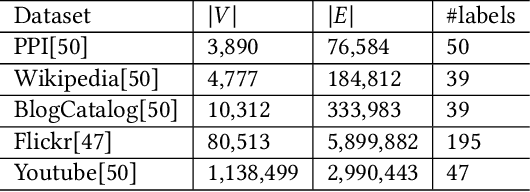
Network embedding has numerous practical applications and has received extensive attention in graph learning, which aims at mapping vertices into a low-dimensional and continuous dense vector space by preserving the underlying structural properties of the graph. Many network embedding methods have been proposed, among which factorization of the Personalized PageRank (PPR for short) matrix has been empirically and theoretically well supported recently. However, several fundamental issues cannot be addressed. (1) Existing methods invoke a seminal Local Push subroutine to approximate \textit{a single} row or column of the PPR matrix. Thus, they have to execute $n$ ($n$ is the number of nodes) Local Push subroutines to obtain a provable PPR matrix, resulting in prohibitively high computational costs for large $n$. (2) The PPR matrix has limited power in capturing the structural similarity between vertices, leading to performance degradation. To overcome these dilemmas, we propose PSNE, an efficient spectral s\textbf{P}arsification method for \textbf{S}caling \textbf{N}etwork \textbf{E}mbedding, which can fast obtain the embedding vectors that retain strong structural similarities. Specifically, PSNE first designs a matrix polynomial sparser to accelerate the calculation of the PPR matrix, which has a theoretical guarantee in terms of the Frobenius norm. Subsequently, PSNE proposes a simple but effective multiple-perspective strategy to enhance further the representation power of the obtained approximate PPR matrix. Finally, PSNE applies a randomized singular value decomposition algorithm on the sparse and multiple-perspective PPR matrix to get the target embedding vectors. Experimental evaluation of real-world and synthetic datasets shows that our solutions are indeed more efficient, effective, and scalable compared with ten competitors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge