Message Passing Neural PDE Solvers

The numerical solution of partial differential equations (PDEs) is difficult, having led to a century of research so far. Recently, there have been pushes to build neural--numerical hybrid solvers, which piggy-backs the modern trend towards fully end-to-end learned systems. Most works so far can only generalize over a subset of properties to which a generic solver would be faced, including: resolution, topology, geometry, boundary conditions, domain discretization regularity, dimensionality, etc. In this work, we build a solver, satisfying these properties, where all the components are based on neural message passing, replacing all heuristically designed components in the computation graph with backprop-optimized neural function approximators. We show that neural message passing solvers representationally contain some classical methods, such as finite differences, finite volumes, and WENO schemes. In order to encourage stability in training autoregressive models, we put forward a method that is based on the principle of zero-stability, posing stability as a domain adaptation problem. We validate our method on various fluid-like flow problems, demonstrating fast, stable, and accurate performance across different domain topologies, discretization, etc. in 1D and 2D. Our model outperforms state-of-the-art numerical solvers in the low resolution regime in terms of speed and accuracy.

Learning Likelihoods with Conditional Normalizing Flows

Normalizing Flows (NFs) are able to model complicated distributions p(y) with strong inter-dimensional correlations and high multimodality by transforming a simple base density p(z) through an invertible neural network under the change of variables formula. Such behavior is desirable in multivariate structured prediction tasks, where handcrafted per-pixel loss-based methods inadequately capture strong correlations between output dimensions. We present a study of conditional normalizing flows (CNFs), a class of NFs where the base density to output space mapping is conditioned on an input x, to model conditional densities p(y|x). CNFs are efficient in sampling and inference, they can be trained with a likelihood-based objective, and CNFs, being generative flows, do not suffer from mode collapse or training instabilities. We provide an effective method to train continuous CNFs for binary problems and in particular, we apply these CNFs to super-resolution and vessel segmentation tasks demonstrating competitive performance on standard benchmark datasets in terms of likelihood and conventional metrics.

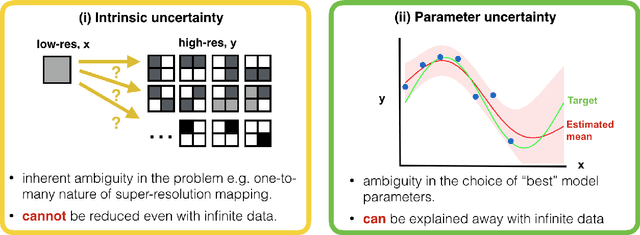
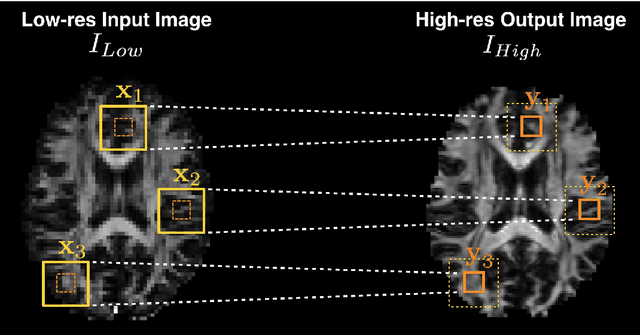
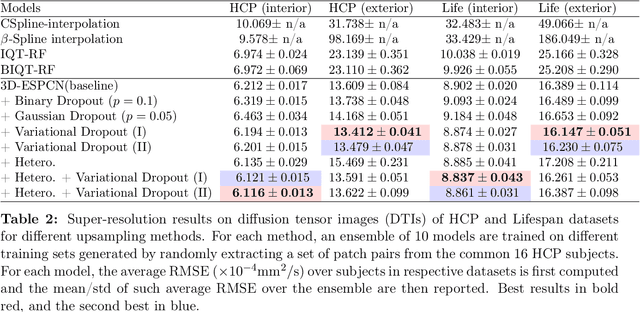
Uncertainty Quantification in Deep Learning for Safer Neuroimage Enhancement

Deep learning (DL) has shown great potential in medical image enhancement problems, such as super-resolution or image synthesis. However, to date, little consideration has been given to uncertainty quantification over the output image. Here we introduce methods to characterise different components of uncertainty in such problems and demonstrate the ideas using diffusion MRI super-resolution. Specifically, we propose to account for $intrinsic$ uncertainty through a heteroscedastic noise model and for $parameter$ uncertainty through approximate Bayesian inference, and integrate the two to quantify $predictive$ uncertainty over the output image. Moreover, we introduce a method to propagate the predictive uncertainty on a multi-channelled image to derived scalar parameters, and separately quantify the effects of intrinsic and parameter uncertainty therein. The methods are evaluated for super-resolution of two different signal representations of diffusion MR images---DTIs and Mean Apparent Propagator MRI---and their derived quantities such as MD and FA, on multiple datasets of both healthy and pathological human brains. Results highlight three key benefits of uncertainty modelling for improving the safety of DL-based image enhancement systems. Firstly, incorporating uncertainty improves the predictive performance even when test data departs from training data. Secondly, the predictive uncertainty highly correlates with errors, and is therefore capable of detecting predictive "failures". Results demonstrate that such an uncertainty measure enables subject-specific and voxel-wise risk assessment of the output images. Thirdly, we show that the method for decomposing predictive uncertainty into its independent sources provides high-level "explanations" for the performance by quantifying how much uncertainty arises from the inherent difficulty of the task or the limited training examples.

Supervised Uncertainty Quantification for Segmentation with Multiple Annotations

The accurate estimation of predictive uncertainty carries importance in medical scenarios such as lung node segmentation. Unfortunately, most existing works on predictive uncertainty do not return calibrated uncertainty estimates, which could be used in practice. In this work we exploit multi-grader annotation variability as a source of 'groundtruth' aleatoric uncertainty, which can be treated as a target in a supervised learning problem. We combine this groundtruth uncertainty with a Probabilistic U-Net and test on the LIDC-IDRI lung nodule CT dataset and MICCAI2012 prostate MRI dataset. We find that we are able to improve predictive uncertainty estimates. We also find that we can improve sample accuracy and sample diversity.

CubeNet: Equivariance to 3D Rotation and Translation

3D Convolutional Neural Networks are sensitive to transformations applied to their input. This is a problem because a voxelized version of a 3D object, and its rotated clone, will look unrelated to each other after passing through to the last layer of a network. Instead, an idealized model would preserve a meaningful representation of the voxelized object, while explaining the pose-difference between the two inputs. An equivariant representation vector has two components: the invariant identity part, and a discernable encoding of the transformation. Models that can't explain pose-differences risk "diluting" the representation, in pursuit of optimizing a classification or regression loss function. We introduce a Group Convolutional Neural Network with linear equivariance to translations and right angle rotations in three dimensions. We call this network CubeNet, reflecting its cube-like symmetry. By construction, this network helps preserve a 3D shape's global and local signature, as it is transformed through successive layers. We apply this network to a variety of 3D inference problems, achieving state-of-the-art on the ModelNet10 classification challenge, and comparable performance on the ISBI 2012 Connectome Segmentation Benchmark. To the best of our knowledge, this is the first 3D rotation equivariant CNN for voxel representations.