The Sparse Recovery Autoencoder

Linear encoding of sparse vectors is widely popular, but is most commonly data-independent -- missing any possible extra (but a-priori unknown) structure beyond sparsity. In this paper we present a new method to learn linear encoders that adapt to data, while still performing well with the widely used $\ell_1$ decoder. The convex $\ell_1$ decoder prevents gradient propagation as needed in standard autoencoder training. Our method is based on the insight that unfolding the convex decoder into $T$ projected gradient steps can address this issue. Our method can be seen as a data-driven way to learn a compressed sensing matrix. Our experiments show that there is indeed additional structure beyond sparsity in several real datasets. Our autoencoder is able to discover it and exploit it to create excellent reconstructions with fewer measurements compared to the previous state of the art methods.

Lattice Rescoring Strategies for Long Short Term Memory Language Models in Speech Recognition

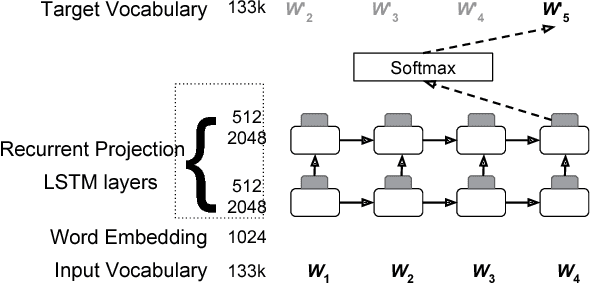
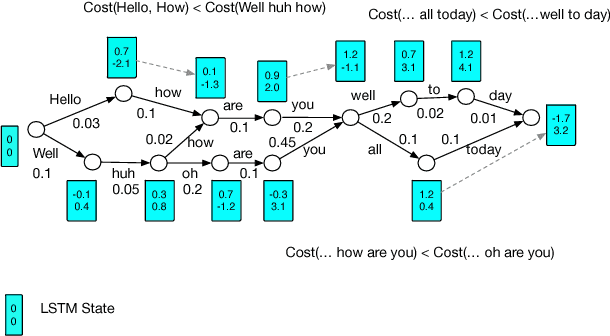
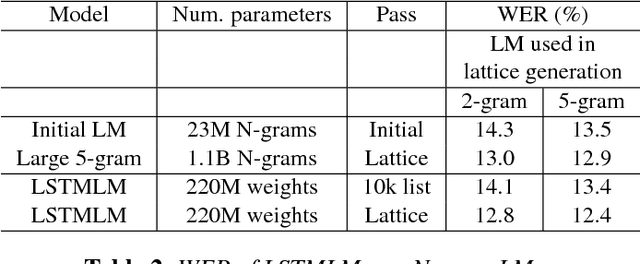
Recurrent neural network (RNN) language models (LMs) and Long Short Term Memory (LSTM) LMs, a variant of RNN LMs, have been shown to outperform traditional N-gram LMs on speech recognition tasks. However, these models are computationally more expensive than N-gram LMs for decoding, and thus, challenging to integrate into speech recognizers. Recent research has proposed the use of lattice-rescoring algorithms using RNNLMs and LSTMLMs as an efficient strategy to integrate these models into a speech recognition system. In this paper, we evaluate existing lattice rescoring algorithms along with new variants on a YouTube speech recognition task. Lattice rescoring using LSTMLMs reduces the word error rate (WER) for this task by 8\% relative to the WER obtained using an N-gram LM.

Orthogonal Random Features

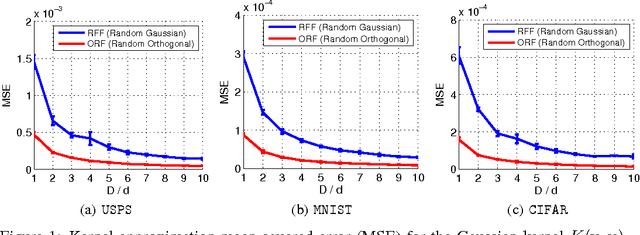
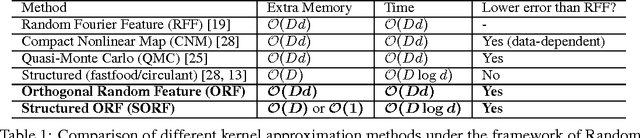
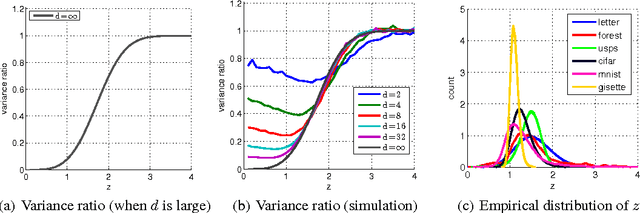
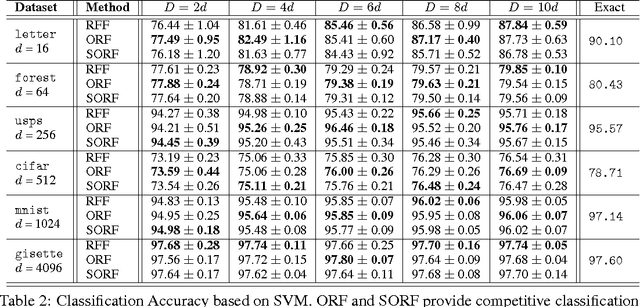
We present an intriguing discovery related to Random Fourier Features: in Gaussian kernel approximation, replacing the random Gaussian matrix by a properly scaled random orthogonal matrix significantly decreases kernel approximation error. We call this technique Orthogonal Random Features (ORF), and provide theoretical and empirical justification for this behavior. Motivated by this discovery, we further propose Structured Orthogonal Random Features (SORF), which uses a class of structured discrete orthogonal matrices to speed up the computation. The method reduces the time cost from $\mathcal{O}(d^2)$ to $\mathcal{O}(d \log d)$, where $d$ is the data dimensionality, with almost no compromise in kernel approximation quality compared to ORF. Experiments on several datasets verify the effectiveness of ORF and SORF over the existing methods. We also provide discussions on using the same type of discrete orthogonal structure for a broader range of applications.