Dmitry Storcheus
The Sparse Recovery Autoencoder
Jul 05, 2018



Abstract:Linear encoding of sparse vectors is widely popular, but is most commonly data-independent -- missing any possible extra (but a-priori unknown) structure beyond sparsity. In this paper we present a new method to learn linear encoders that adapt to data, while still performing well with the widely used $\ell_1$ decoder. The convex $\ell_1$ decoder prevents gradient propagation as needed in standard autoencoder training. Our method is based on the insight that unfolding the convex decoder into $T$ projected gradient steps can address this issue. Our method can be seen as a data-driven way to learn a compressed sensing matrix. Our experiments show that there is indeed additional structure beyond sparsity in several real datasets. Our autoencoder is able to discover it and exploit it to create excellent reconstructions with fewer measurements compared to the previous state of the art methods.
Foundations of Coupled Nonlinear Dimensionality Reduction
Nov 25, 2015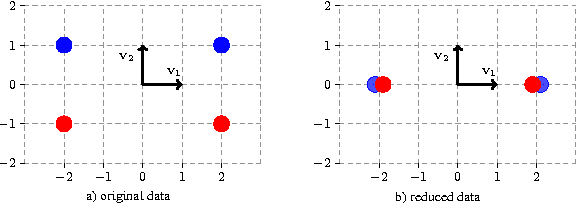
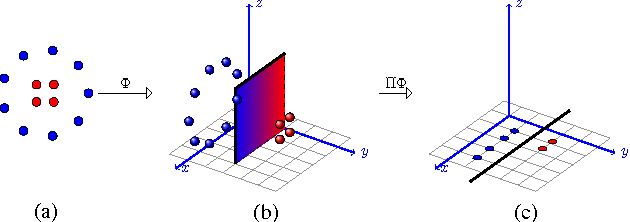
Abstract:In this paper we introduce and analyze the learning scenario of \emph{coupled nonlinear dimensionality reduction}, which combines two major steps of machine learning pipeline: projection onto a manifold and subsequent supervised learning. First, we present new generalization bounds for this scenario and, second, we introduce an algorithm that follows from these bounds. The generalization error bound is based on a careful analysis of the empirical Rademacher complexity of the relevant hypothesis set. In particular, we show an upper bound on the Rademacher complexity that is in $\widetilde O(\sqrt{\Lambda_{(r)}/m})$, where $m$ is the sample size and $\Lambda_{(r)}$ the upper bound on the Ky-Fan $r$-norm of the associated kernel matrix. We give both upper and lower bound guarantees in terms of that Ky-Fan $r$-norm, which strongly justifies the definition of our hypothesis set. To the best of our knowledge, these are the first learning guarantees for the problem of coupled dimensionality reduction. Our analysis and learning guarantees further apply to several special cases, such as that of using a fixed kernel with supervised dimensionality reduction or that of unsupervised learning of a kernel for dimensionality reduction followed by a supervised learning algorithm. Based on theoretical analysis, we suggest a structural risk minimization algorithm consisting of the coupled fitting of a low dimensional manifold and a separation function on that manifold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge