Orthogonal Random Features
Paper and Code
Oct 28, 2016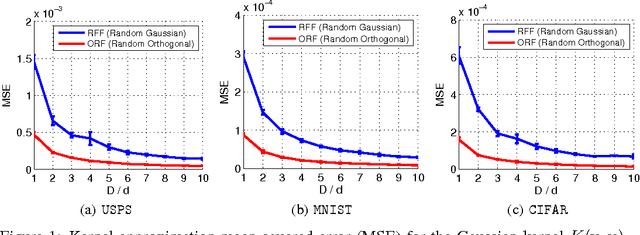
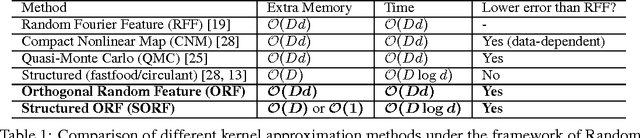
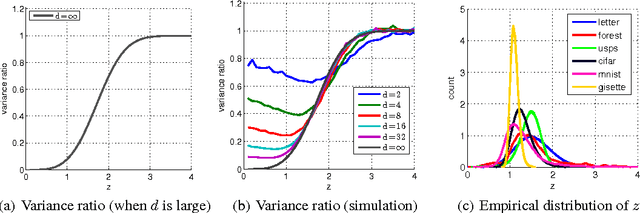
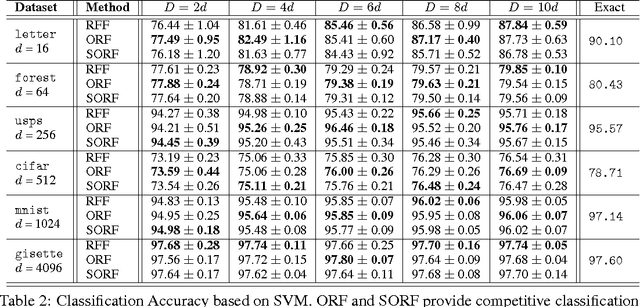
We present an intriguing discovery related to Random Fourier Features: in Gaussian kernel approximation, replacing the random Gaussian matrix by a properly scaled random orthogonal matrix significantly decreases kernel approximation error. We call this technique Orthogonal Random Features (ORF), and provide theoretical and empirical justification for this behavior. Motivated by this discovery, we further propose Structured Orthogonal Random Features (SORF), which uses a class of structured discrete orthogonal matrices to speed up the computation. The method reduces the time cost from $\mathcal{O}(d^2)$ to $\mathcal{O}(d \log d)$, where $d$ is the data dimensionality, with almost no compromise in kernel approximation quality compared to ORF. Experiments on several datasets verify the effectiveness of ORF and SORF over the existing methods. We also provide discussions on using the same type of discrete orthogonal structure for a broader range of applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge