Multi-Scale Feature Fusion with Image-Driven Spatial Integration for Left Atrium Segmentation from Cardiac MRI Images

Accurate segmentation of the left atrium (LA) from late gadolinium-enhanced magnetic resonance imaging plays a vital role in visualizing diseased atrial structures, enabling the diagnosis and management of cardiovascular diseases. It is particularly essential for planning treatment with ablation therapy, a key intervention for atrial fibrillation (AF). However, manual segmentation is time-intensive and prone to inter-observer variability, underscoring the need for automated solutions. Class-agnostic foundation models like DINOv2 have demonstrated remarkable feature extraction capabilities in vision tasks. However, their lack of domain specificity and task-specific adaptation can reduce spatial resolution during feature extraction, impacting the capture of fine anatomical detail in medical imaging. To address this limitation, we propose a segmentation framework that integrates DINOv2 as an encoder with a UNet-style decoder, incorporating multi-scale feature fusion and input image integration to enhance segmentation accuracy. The learnable weighting mechanism dynamically prioritizes hierarchical features from different encoder blocks of the foundation model, optimizing feature selection for task relevance. Additionally, the input image is reintroduced during the decoding stage to preserve high-resolution spatial details, addressing limitations of downsampling in the encoder. We validate our approach on the LAScarQS 2022 dataset and demonstrate improved performance with a 92.3% Dice and 84.1% IoU score for giant architecture compared to the nnUNet baseline model. These findings emphasize the efficacy of our approach in advancing the field of automated left atrium segmentation from cardiac MRI.

Active Label Refinement for Robust Training of Imbalanced Medical Image Classification Tasks in the Presence of High Label Noise

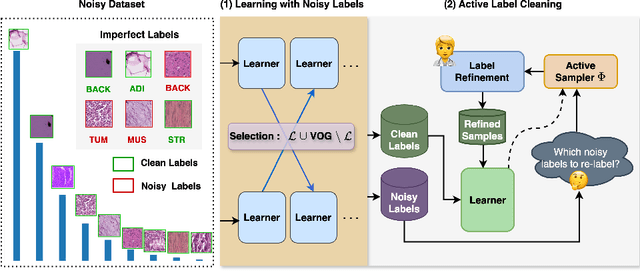
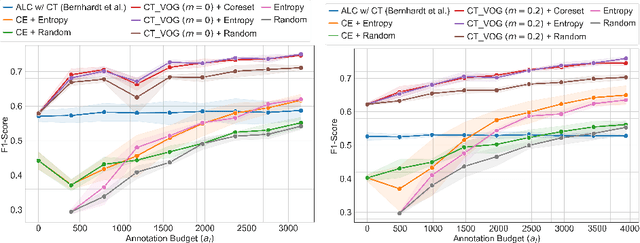
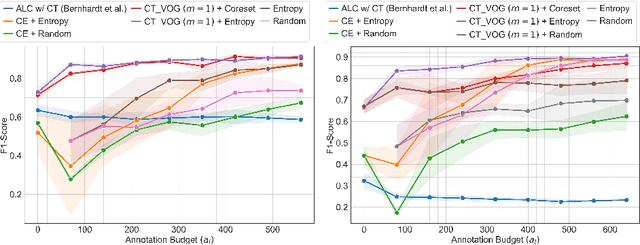
The robustness of supervised deep learning-based medical image classification is significantly undermined by label noise. Although several methods have been proposed to enhance classification performance in the presence of noisy labels, they face some challenges: 1) a struggle with class-imbalanced datasets, leading to the frequent overlooking of minority classes as noisy samples; 2) a singular focus on maximizing performance using noisy datasets, without incorporating experts-in-the-loop for actively cleaning the noisy labels. To mitigate these challenges, we propose a two-phase approach that combines Learning with Noisy Labels (LNL) and active learning. This approach not only improves the robustness of medical image classification in the presence of noisy labels, but also iteratively improves the quality of the dataset by relabeling the important incorrect labels, under a limited annotation budget. Furthermore, we introduce a novel Variance of Gradients approach in LNL phase, which complements the loss-based sample selection by also sampling under-represented samples. Using two imbalanced noisy medical classification datasets, we demonstrate that that our proposed technique is superior to its predecessors at handling class imbalance by not misidentifying clean samples from minority classes as mostly noisy samples.

How does self-supervised pretraining improve robustness against noisy labels across various medical image classification datasets?

Noisy labels can significantly impact medical image classification, particularly in deep learning, by corrupting learned features. Self-supervised pretraining, which doesn't rely on labeled data, can enhance robustness against noisy labels. However, this robustness varies based on factors like the number of classes, dataset complexity, and training size. In medical images, subtle inter-class differences and modality-specific characteristics add complexity. Previous research hasn't comprehensively explored the interplay between self-supervised learning and robustness against noisy labels in medical image classification, considering all these factors. In this study, we address three key questions: i) How does label noise impact various medical image classification datasets? ii) Which types of medical image datasets are more challenging to learn and more affected by label noise? iii) How do different self-supervised pretraining methods enhance robustness across various medical image datasets? Our results show that DermNet, among five datasets (Fetal plane, DermNet, COVID-DU-Ex, MURA, NCT-CRC-HE-100K), is the most challenging but exhibits greater robustness against noisy labels. Additionally, contrastive learning stands out among the eight self-supervised methods as the most effective approach to enhance robustness against noisy labels.

A Distance Map Regularized CNN for Cardiac Cine MR Image Segmentation

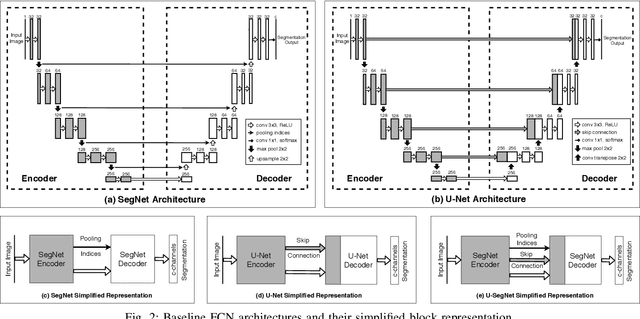
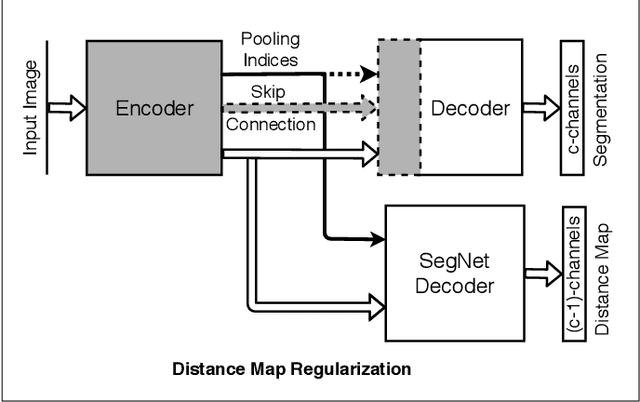
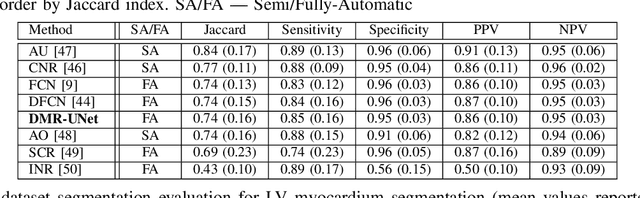
Cardiac image segmentation is a critical process for generating personalized models of the heart and for quantifying cardiac performance parameters. Several convolutional neural network (CNN) architectures have been proposed to segment the heart chambers from cardiac cine MR images. Here we propose a multi-task learning (MTL)-based regularization framework for cardiac MR image segmentation. The network is trained to perform the main task of semantic segmentation, along with a simultaneous, auxiliary task of pixel-wise distance map regression. The proposed distance map regularizer is a decoder network added to the bottleneck layer of an existing CNN architecture, facilitating the network to learn robust global features. The regularizer block is removed after training, so that the original number of network parameters does not change. We show that the proposed regularization method improves both binary and multi-class segmentation performance over the corresponding state-of-the-art CNN architectures on two publicly available cardiac cine MRI datasets, obtaining average dice coefficient of 0.84$\pm$0.03 and 0.91$\pm$0.04, respectively. Furthermore, we also demonstrate improved generalization performance of the distance map regularized network on cross-dataset segmentation, showing as much as 41% improvement in average Dice coefficient from 0.57$\pm$0.28 to 0.80$\pm$0.13.