Explain Like I'm Five: Using LLMs to Improve PDE Surrogate Models with Text

Solving Partial Differential Equations (PDEs) is ubiquitous in science and engineering. Computational complexity and difficulty in writing numerical solvers has motivated the development of machine learning techniques to generate solutions quickly. Many existing methods are purely data driven, relying solely on numerical solution fields, rather than known system information such as boundary conditions and governing equations. However, the recent rise in popularity of Large Language Models (LLMs) has enabled easy integration of text in multimodal machine learning models. In this work, we use pretrained LLMs to integrate various amounts known system information into PDE learning. Our multimodal approach significantly outperforms our baseline model, FactFormer, in both next-step prediction and autoregressive rollout performance on the 2D Heat, Burgers, Navier-Stokes, and Shallow Water equations. Further analysis shows that pretrained LLMs provide highly structured latent space that is consistent with the amount of system information provided through text.

Strategies for Pretraining Neural Operators

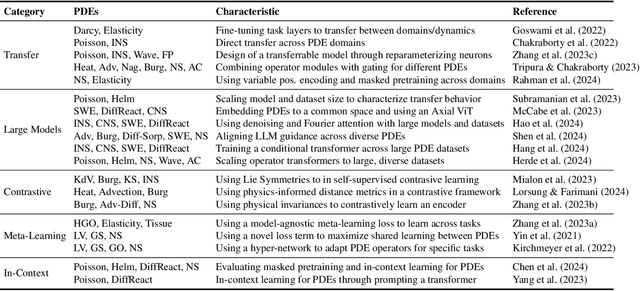
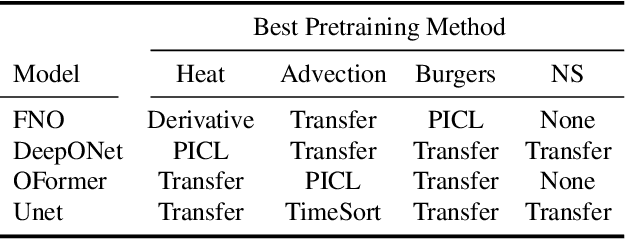
Pretraining for partial differential equation (PDE) modeling has recently shown promise in scaling neural operators across datasets to improve generalizability and performance. Despite these advances, our understanding of how pretraining affects neural operators is still limited; studies generally propose tailored architectures and datasets that make it challenging to compare or examine different pretraining frameworks. To address this, we compare various pretraining methods without optimizing architecture choices to characterize pretraining dynamics on different models and datasets as well as to understand its scaling and generalization behavior. We find that pretraining is highly dependent on model and dataset choices, but in general transfer learning or physics-based pretraining strategies work best. In addition, pretraining performance can be further improved by using data augmentations. Lastly, pretraining is additionally beneficial when fine-tuning in scarce data regimes or when generalizing to downstream data similar to the pretraining distribution. Through providing insights into pretraining neural operators for physics prediction, we hope to motivate future work in developing and evaluating pretraining methods for PDEs.

PICL: Physics Informed Contrastive Learning for Partial Differential Equations

Neural operators have recently grown in popularity as Partial Differential Equation (PDEs) surrogate models. Learning solution functionals, rather than functions, has proven to be a powerful approach to calculate fast, accurate solutions to complex PDEs. While much work has been done evaluating neural operator performance on a wide variety of surrogate modeling tasks, these works normally evaluate performance on a single equation at a time. In this work, we develop a novel contrastive pretraining framework utilizing Generalized Contrastive Loss that improves neural operator generalization across multiple governing equations simultaneously. Governing equation coefficients are used to measure ground-truth similarity between systems. A combination of physics-informed system evolution and latent-space model output are anchored to input data and used in our distance function. We find that physics-informed contrastive pretraining improves both accuracy and generalization for the Fourier Neural Operator in fixed-future task, with comparable performance on the autoregressive rollout, and superresolution tasks for the 1D Heat, Burgers', and linear advection equations.

Physics Informed Token Transformer

Solving Partial Differential Equations (PDEs) is the core of many fields of science and engineering. While classical approaches are often prohibitively slow, machine learning models often fail to incorporate complete system information. Over the past few years, transformers have had a significant impact on the field of Artificial Intelligence and have seen increased usage in PDE applications. However, despite their success, transformers currently lack integration with physics and reasoning. This study aims to address this issue by introducing PITT: Physics Informed Token Transformer. The purpose of PITT is to incorporate the knowledge of physics by embedding partial differential equations (PDEs) into the learning process. PITT uses an equation tokenization method to learn an analytically-driven numerical update operator. By tokenizing PDEs and embedding partial derivatives, the transformer models become aware of the underlying knowledge behind physical processes. To demonstrate this, PITT is tested on challenging PDE neural operators in both 1D and 2D prediction tasks. The results show that PITT outperforms the popular Fourier Neural Operator and has the ability to extract physically relevant information from governing equations.

Neural Network Predicts Ion Concentration Profiles under Nanoconfinement

Modeling the ion concentration profile in nanochannel plays an important role in understanding the electrical double layer and electroosmotic flow. Due to the non-negligible surface interaction and the effect of discrete solvent molecules, molecular dynamics (MD) simulation is often used as an essential tool to study the behavior of ions under nanoconfinement. Despite the accuracy of MD simulation in modeling nanoconfinement systems, it is computationally expensive. In this work, we propose neural network to predict ion concentration profiles in nanochannels with different configurations, including channel widths, ion molarity, and ion types. By modeling the ion concentration profile as a probability distribution, our neural network can serve as a much faster surrogate model for MD simulation with high accuracy. We further demonstrate the superior prediction accuracy of neural network over XGBoost. Lastly, we demonstrated that neural network is flexible in predicting ion concentration profiles with different bin sizes. Overall, our deep learning model is a fast, flexible, and accurate surrogate model to predict ion concentration profiles in nanoconfinement.

MeshDQN: A Deep Reinforcement Learning Framework for Improving Meshes in Computational Fluid Dynamics

Meshing is a critical, but user-intensive process necessary for stable and accurate simulations in computational fluid dynamics (CFD). Mesh generation is often a bottleneck in CFD pipelines. Adaptive meshing techniques allow the mesh to be updated automatically to produce an accurate solution for the problem at hand. Existing classical techniques for adaptive meshing require either additional functionality out of solvers, many training simulations, or both. Current machine learning techniques often require substantial computational cost for training data generation, and are restricted in scope to the training data flow regime. MeshDQN is developed as a general purpose deep reinforcement learning framework to iteratively coarsen meshes while preserving target property calculation. A graph neural network based deep Q network is used to select mesh vertices for removal and solution interpolation is used to bypass expensive simulations at each step in the improvement process. MeshDQN requires a single simulation prior to mesh coarsening, while making no assumptions about flow regime, mesh type, or solver, only requiring the ability to modify meshes directly in a CFD pipeline. MeshDQN successfully improves meshes for two 2D airfoils.

AugLiChem: Data Augmentation Library of Chemical Structures for Machine Learning

Machine learning (ML) has demonstrated the promise for accurate and efficient property prediction of molecules and crystalline materials. To develop highly accurate ML models for chemical structure property prediction, datasets with sufficient samples are required. However, obtaining clean and sufficient data of chemical properties can be expensive and time-consuming, which greatly limits the performance of ML models. Inspired by the success of data augmentations in computer vision and natural language processing, we developed AugLiChem: the data augmentation library for chemical structures. Augmentation methods for both crystalline systems and molecules are introduced, which can be utilized for fingerprint-based ML models and Graph Neural Networks(GNNs). We show that using our augmentation strategies significantly improves the performance of ML models, especially when using GNNs. In addition, the augmentations that we developed can be used as a direct plug-in module during training and have demonstrated the effectiveness when implemented with different GNN models through the AugliChem library. The Python-based package for our implementation of Auglichem: Data augmentation library for chemical structures, is publicly available at: https://github.com/BaratiLab/AugLiChem.

Learned Uncertainty-Aware (LUNA) Bases for Bayesian Regression using Multi-Headed Auxiliary Networks

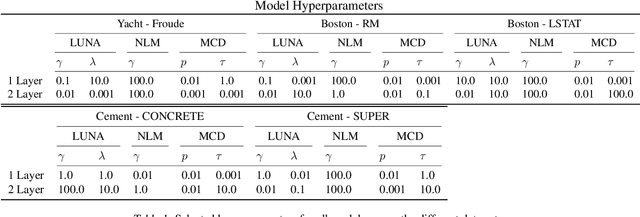
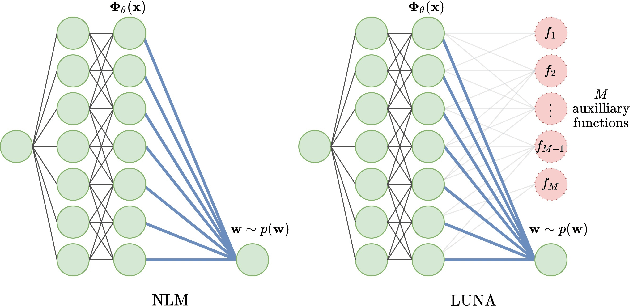
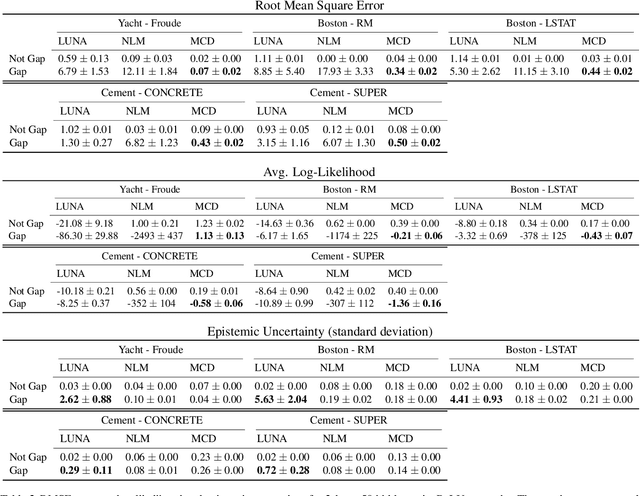
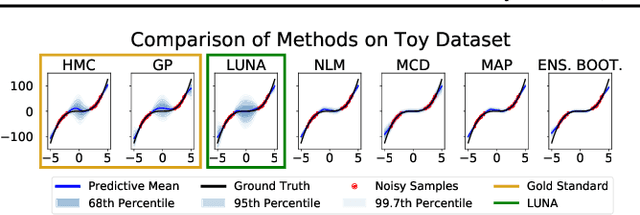
Neural Linear Models (NLM) are deep models that produce predictive uncertainty by learning features from the data and then performing Bayesian linear regression over these features. Despite their popularity, few works have focused on formally evaluating the predictive uncertainties of these models. In this work, we show that traditional training procedures for NLMs can drastically underestimate uncertainty in data-scarce regions. We identify the underlying reasons for this behavior and propose a novel training procedure for capturing useful predictive uncertainties.