Coupled Diffusion-Encoder Models for Reconstruction of Flow Fields

Data-driven flow-field reconstruction typically relies on autoencoder architectures that compress high-dimensional states into low-dimensional latent representations. However, classical approaches such as variational autoencoders (VAEs) often struggle to preserve the higher-order statistical structure of fluid flows when subjected to strong compression. We propose DiffCoder, a coupled framework that integrates a probabilistic diffusion model with a conventional convolutional ResNet encoder and trains both components end-to-end. The encoder compresses the flow field into a latent representation, while the diffusion model learns a generative prior over reconstructions conditioned on the compressed state. This design allows DiffCoder to recover distributional and spectral properties that are not strictly required for minimizing pointwise reconstruction loss but are critical for faithfully representing statistical properties of the flow field. We evaluate DiffCoder and VAE baselines across multiple model sizes and compression ratios on a challenging dataset of Kolmogorov flow fields. Under aggressive compression, DiffCoder significantly improves the spectral accuracy while VAEs exhibit substantial degradation. Although both methods show comparable relative L2 reconstruction error, DiffCoder better preserves the underlying distributional structure of the flow. At moderate compression levels, sufficiently large VAEs remain competitive, suggesting that diffusion-based priors provide the greatest benefit when information bottlenecks are severe. These results demonstrate that the generative decoding by diffusion offers a promising path toward compact, statistically consistent representations of complex flow fields.

Pretraining a Neural Operator in Lower Dimensions

There has recently been increasing attention towards developing foundational neural Partial Differential Equation (PDE) solvers and neural operators through large-scale pretraining. However, unlike vision and language models that make use of abundant and inexpensive (unlabeled) data for pretraining, these neural solvers usually rely on simulated PDE data, which can be costly to obtain, especially for high-dimensional PDEs. In this work, we aim to Pretrain neural PDE solvers on Lower Dimensional PDEs (PreLowD) where data collection is the least expensive. We evaluated the effectiveness of this pretraining strategy in similar PDEs in higher dimensions. We use the Factorized Fourier Neural Operator (FFNO) due to having the necessary flexibility to be applied to PDE data of arbitrary spatial dimensions and reuse trained parameters in lower dimensions. In addition, our work sheds light on the effect of the fine-tuning configuration to make the most of this pretraining strategy.

Strategies for Pretraining Neural Operators

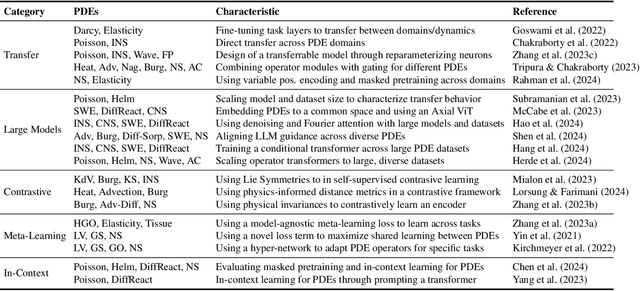
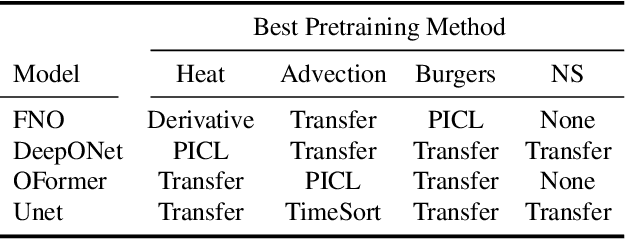
Pretraining for partial differential equation (PDE) modeling has recently shown promise in scaling neural operators across datasets to improve generalizability and performance. Despite these advances, our understanding of how pretraining affects neural operators is still limited; studies generally propose tailored architectures and datasets that make it challenging to compare or examine different pretraining frameworks. To address this, we compare various pretraining methods without optimizing architecture choices to characterize pretraining dynamics on different models and datasets as well as to understand its scaling and generalization behavior. We find that pretraining is highly dependent on model and dataset choices, but in general transfer learning or physics-based pretraining strategies work best. In addition, pretraining performance can be further improved by using data augmentations. Lastly, pretraining is additionally beneficial when fine-tuning in scarce data regimes or when generalizing to downstream data similar to the pretraining distribution. Through providing insights into pretraining neural operators for physics prediction, we hope to motivate future work in developing and evaluating pretraining methods for PDEs.

Multi-scale Time-stepping of Partial Differential Equations with Transformers

Developing fast surrogates for Partial Differential Equations (PDEs) will accelerate design and optimization in almost all scientific and engineering applications. Neural networks have been receiving ever-increasing attention and demonstrated remarkable success in computational modeling of PDEs, however; their prediction accuracy is not at the level of full deployment. In this work, we utilize the transformer architecture, the backbone of numerous state-of-the-art AI models, to learn the dynamics of physical systems as the mixing of spatial patterns learned by a convolutional autoencoder. Moreover, we incorporate the idea of multi-scale hierarchical time-stepping to increase the prediction speed and decrease accumulated error over time. Our model achieves similar or better results in predicting the time-evolution of Navier-Stokes equations compared to the powerful Fourier Neural Operator (FNO) and two transformer-based neural operators OFormer and Galerkin Transformer.

Surrogate Modeling of Melt Pool Thermal Field using Deep Learning

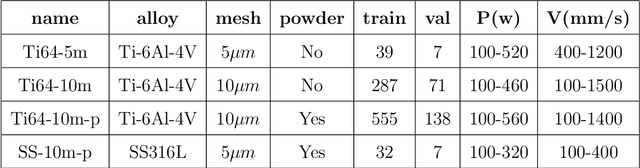
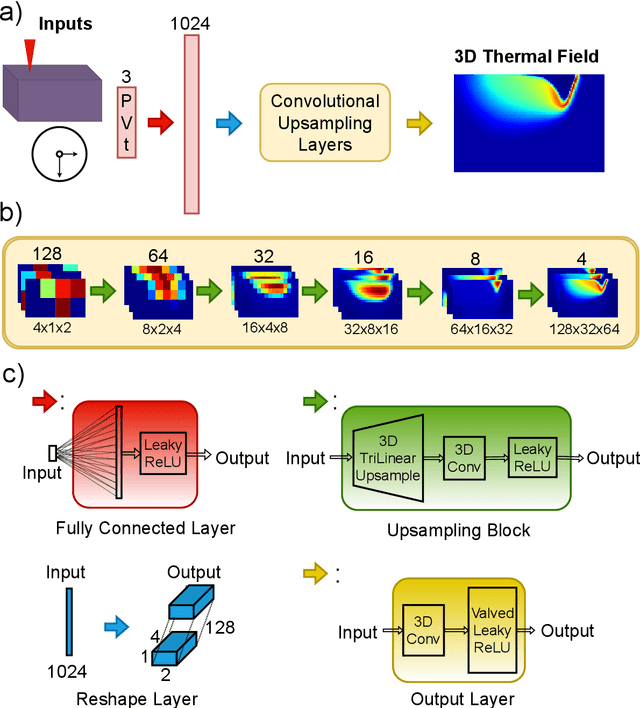
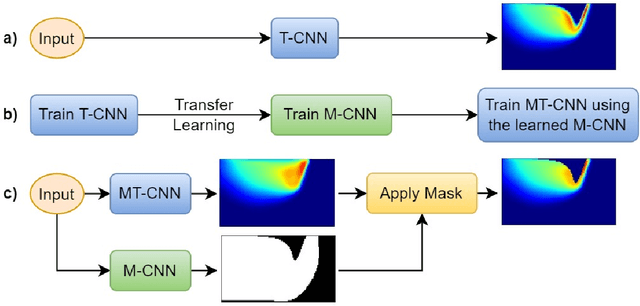
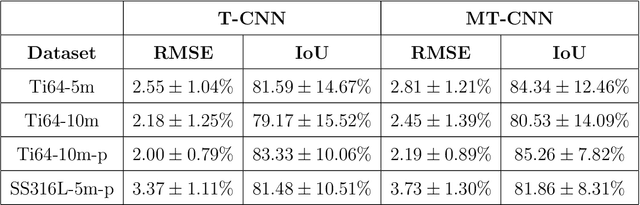
Powder-based additive manufacturing has transformed the manufacturing industry over the last decade. In Laser Powder Bed Fusion, a specific part is built in an iterative manner in which two-dimensional cross-sections are formed on top of each other by melting and fusing the proper areas of the powder bed. In this process, the behavior of the melt pool and its thermal field has a very important role in predicting the quality of the manufactured part and its possible defects. However, the simulation of such a complex phenomenon is usually very time-consuming and requires huge computational resources. Flow-3D is one of the software packages capable of executing such simulations using iterative numerical solvers. In this work, we create three datasets of single-trail processes using Flow-3D and use them to train a convolutional neural network capable of predicting the behavior of the three-dimensional thermal field of the melt pool solely by taking three parameters as input: laser power, laser velocity, and time step. The CNN achieves a relative Root Mean Squared Error of 2% to 3% for the temperature field and an average Intersection over Union score of 80% to 90% in predicting the melt pool area. Moreover, since time is included as one of the inputs of the model, the thermal field can be instantly obtained for any arbitrary time step without the need to iterate and compute all the steps