BlastOFormer: Attention and Neural Operator Deep Learning Methods for Explosive Blast Prediction

Accurate prediction of blast pressure fields is essential for applications in structural safety, defense planning, and hazard mitigation. Traditional methods such as empirical models and computational fluid dynamics (CFD) simulations offer limited trade offs between speed and accuracy; empirical models fail to capture complex interactions in cluttered environments, while CFD simulations are computationally expensive and time consuming. In this work, we introduce BlastOFormer, a novel Transformer based surrogate model for full field maximum pressure prediction from arbitrary obstacle and charge configurations. BlastOFormer leverages a signed distance function (SDF) encoding and a grid to grid attention based architecture inspired by OFormer and Vision Transformer (ViT) frameworks. Trained on a dataset generated using the open source blastFoam CFD solver, our model outperforms convolutional neural networks (CNNs) and Fourier Neural Operators (FNOs) across both log transformed and unscaled domains. Quantitatively, BlastOFormer achieves the highest R2 score (0.9516) and lowest error metrics, while requiring only 6.4 milliseconds for inference, more than 600,000 times faster than CFD simulations. Qualitative visualizations and error analyses further confirm BlastOFormer's superior spatial coherence and generalization capabilities. These results highlight its potential as a real time alternative to conventional CFD approaches for blast pressure estimation in complex environments.

Neural Functional: Learning Function to Scalar Maps for Neural PDE Surrogates

Many architectures for neural PDE surrogates have been proposed in recent years, largely based on neural networks or operator learning. In this work, we derive and propose a new architecture, the Neural Functional, which learns function to scalar mappings. Its implementation leverages insights from operator learning and neural fields, and we show the ability of neural functionals to implicitly learn functional derivatives. For the first time, this allows for an extension of Hamiltonian mechanics to neural PDE surrogates by learning the Hamiltonian functional and optimizing its functional derivatives. We demonstrate that the Hamiltonian Neural Functional can be an effective surrogate model through improved stability and conserving energy-like quantities on 1D and 2D PDEs. Beyond PDEs, functionals are prevalent in physics; functional approximation and learning with its gradients may find other uses, such as in molecular dynamics or design optimization.

Generative Latent Neural PDE Solver using Flow Matching

Autoregressive next-step prediction models have become the de-facto standard for building data-driven neural solvers to forecast time-dependent partial differential equations (PDEs). Denoise training that is closely related to diffusion probabilistic model has been shown to enhance the temporal stability of neural solvers, while its stochastic inference mechanism enables ensemble predictions and uncertainty quantification. In principle, such training involves sampling a series of discretized diffusion timesteps during both training and inference, inevitably increasing computational overhead. In addition, most diffusion models apply isotropic Gaussian noise on structured, uniform grids, limiting their adaptability to irregular domains. We propose a latent diffusion model for PDE simulation that embeds the PDE state in a lower-dimensional latent space, which significantly reduces computational costs. Our framework uses an autoencoder to map different types of meshes onto a unified structured latent grid, capturing complex geometries. By analyzing common diffusion paths, we propose to use a coarsely sampled noise schedule from flow matching for both training and testing. Numerical experiments show that the proposed model outperforms several deterministic baselines in both accuracy and long-term stability, highlighting the potential of diffusion-based approaches for robust data-driven PDE learning.

Predicting Change, Not States: An Alternate Framework for Neural PDE Surrogates

Neural surrogates for partial differential equations (PDEs) have become popular due to their potential to quickly simulate physics. With a few exceptions, neural surrogates generally treat the forward evolution of time-dependent PDEs as a black box by directly predicting the next state. While this is a natural and easy framework for applying neural surrogates, it can be an over-simplified and rigid framework for predicting physics. In this work, we propose an alternative framework in which neural solvers predict the temporal derivative and an ODE integrator forwards the solution in time, which has little overhead and is broadly applicable across model architectures and PDEs. We find that by simply changing the training target and introducing numerical integration during inference, neural surrogates can gain accuracy and stability. Predicting temporal derivatives also allows models to not be constrained to a specific temporal discretization, allowing for flexible time-stepping during inference or training on higher-resolution PDE data. Lastly, we investigate why this new framework can be beneficial and in what situations does it work well.

Text2PDE: Latent Diffusion Models for Accessible Physics Simulation

Recent advances in deep learning have inspired numerous works on data-driven solutions to partial differential equation (PDE) problems. These neural PDE solvers can often be much faster than their numerical counterparts; however, each presents its unique limitations and generally balances training cost, numerical accuracy, and ease of applicability to different problem setups. To address these limitations, we introduce several methods to apply latent diffusion models to physics simulation. Firstly, we introduce a mesh autoencoder to compress arbitrarily discretized PDE data, allowing for efficient diffusion training across various physics. Furthermore, we investigate full spatio-temporal solution generation to mitigate autoregressive error accumulation. Lastly, we investigate conditioning on initial physical quantities, as well as conditioning solely on a text prompt to introduce text2PDE generation. We show that language can be a compact, interpretable, and accurate modality for generating physics simulations, paving the way for more usable and accessible PDE solvers. Through experiments on both uniform and structured grids, we show that the proposed approach is competitive with current neural PDE solvers in both accuracy and efficiency, with promising scaling behavior up to $\sim$3 billion parameters. By introducing a scalable, accurate, and usable physics simulator, we hope to bring neural PDE solvers closer to practical use.

Strategies for Pretraining Neural Operators

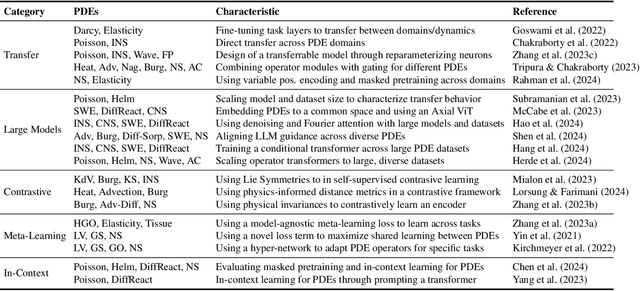
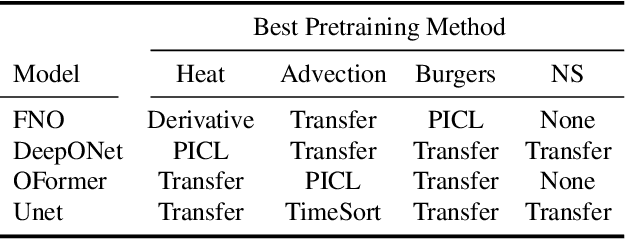
Pretraining for partial differential equation (PDE) modeling has recently shown promise in scaling neural operators across datasets to improve generalizability and performance. Despite these advances, our understanding of how pretraining affects neural operators is still limited; studies generally propose tailored architectures and datasets that make it challenging to compare or examine different pretraining frameworks. To address this, we compare various pretraining methods without optimizing architecture choices to characterize pretraining dynamics on different models and datasets as well as to understand its scaling and generalization behavior. We find that pretraining is highly dependent on model and dataset choices, but in general transfer learning or physics-based pretraining strategies work best. In addition, pretraining performance can be further improved by using data augmentations. Lastly, pretraining is additionally beneficial when fine-tuning in scarce data regimes or when generalizing to downstream data similar to the pretraining distribution. Through providing insights into pretraining neural operators for physics prediction, we hope to motivate future work in developing and evaluating pretraining methods for PDEs.

CaFA: Global Weather Forecasting with Factorized Attention on Sphere

Accurate weather forecasting is crucial in various sectors, impacting decision-making processes and societal events. Data-driven approaches based on machine learning models have recently emerged as a promising alternative to numerical weather prediction models given their potential to capture physics of different scales from historical data and the significantly lower computational cost during the prediction stage. Renowned for its state-of-the-art performance across diverse domains, the Transformer model has also gained popularity in machine learning weather prediction. Yet applying Transformer architectures to weather forecasting, particularly on a global scale is computationally challenging due to the quadratic complexity of attention and the quadratic increase in spatial points as resolution increases. In this work, we propose a factorized-attention-based model tailored for spherical geometries to mitigate this issue. More specifically, it utilizes multi-dimensional factorized kernels that convolve over different axes where the computational complexity of the kernel is only quadratic to the axial resolution instead of overall resolution. The deterministic forecasting accuracy of the proposed model on $1.5^\circ$ and 0-7 days' lead time is on par with state-of-the-art purely data-driven machine learning weather prediction models. We also showcase the proposed model holds great potential to push forward the Pareto front of accuracy-efficiency for Transformer weather models, where it can achieve better accuracy with less computational cost compared to Transformer based models with standard attention.

Masked Autoencoders are PDE Learners

Neural solvers for partial differential equations (PDEs) have great potential, yet their practicality is currently limited by their generalizability. PDEs evolve over broad scales and exhibit diverse behaviors; predicting these phenomena will require learning representations across a wide variety of inputs, which may encompass different coefficients, geometries, or equations. As a step towards generalizable PDE modeling, we adapt masked pretraining for PDEs. Through self-supervised learning across PDEs, masked autoencoders can learn useful latent representations for downstream tasks. In particular, masked pretraining can improve coefficient regression and timestepping performance of neural solvers on unseen equations. We hope that masked pretraining can emerge as a unifying method across large, unlabeled, and heterogeneous datasets to learn latent physics at scale.

FaultFormer: Transformer-based Prediction of Bearing Faults

The growth of deep learning in the past decade has motivated important applications to smart manufacturing and machine health monitoring. In particular, vibration data offers a rich and reliable source to provide meaningful insights into machine health and predictive maintenance. In this work, we present a Transformer based framework for analyzing vibration signals to predict different types of bearing faults (FaultFormer). In particular, we process signal data using data augmentations and extract their Fourier modes to train a transformer encoder to achieve state of the art accuracies. The attention mechanism as well as model outputs were analyzed to confirm the transformer's ability to automatically extract features within signals and learn both global and local relationships to make classifications. Lastly, two pretraining strategies were proposed to pave the way for large, generalizable transformers that could adapt to new data, situations, or machinery on the production floor.