Towards Model-Agnostic Posterior Approximation for Fast and Accurate Variational Autoencoders

Inference for Variational Autoencoders (VAEs) consists of learning two models: (1) a generative model, which transforms a simple distribution over a latent space into the distribution over observed data, and (2) an inference model, which approximates the posterior of the latent codes given data. The two components are learned jointly via a lower bound to the generative model's log marginal likelihood. In early phases of joint training, the inference model poorly approximates the latent code posteriors. Recent work showed that this leads optimization to get stuck in local optima, negatively impacting the learned generative model. As such, recent work suggests ensuring a high-quality inference model via iterative training: maximizing the objective function relative to the inference model before every update to the generative model. Unfortunately, iterative training is inefficient, requiring heuristic criteria for reverting from iterative to joint training for speed. Here, we suggest an inference method that trains the generative and inference models independently. It approximates the posterior of the true model a priori; fixing this posterior approximation, we then maximize the lower bound relative to only the generative model. By conventional wisdom, this approach should rely on the true prior and likelihood of the true model to approximate its posterior (which are unknown). However, we show that we can compute a deterministic, model-agnostic posterior approximation (MAPA) of the true model's posterior. We then use MAPA to develop a proof-of-concept inference method. We present preliminary results on low-dimensional synthetic data that (1) MAPA captures the trend of the true posterior, and (2) our MAPA-based inference performs better density estimation with less computation than baselines. Lastly, we present a roadmap for scaling the MAPA-based inference method to high-dimensional data.

An Empirical Analysis of the Advantages of Finite- v.s. Infinite-Width Bayesian Neural Networks

Comparing Bayesian neural networks (BNNs) with different widths is challenging because, as the width increases, multiple model properties change simultaneously, and, inference in the finite-width case is intractable. In this work, we empirically compare finite- and infinite-width BNNs, and provide quantitative and qualitative explanations for their performance difference. We find that when the model is mis-specified, increasing width can hurt BNN performance. In these cases, we provide evidence that finite-width BNNs generalize better partially due to the properties of their frequency spectrum that allows them to adapt under model mismatch.

Failure Modes of Variational Autoencoders and Their Effects on Downstream Tasks

Variational Auto-encoders (VAEs) are deep generative latent variable models that are widely used for a number of downstream tasks. While it has been demonstrated that VAE training can suffer from a number of pathologies, existing literature lacks characterizations of exactly when these pathologies occur and how they impact down-stream task performance. In this paper we concretely characterize conditions under which VAE training exhibits pathologies and connect these failure modes to undesirable effects on specific downstream tasks - learning compressed and disentangled representations, adversarial robustness and semi-supervised learning.

BaCOUn: Bayesian Classifers with Out-of-Distribution Uncertainty

Traditional training of deep classifiers yields overconfident models that are not reliable under dataset shift. We propose a Bayesian framework to obtain reliable uncertainty estimates for deep classifiers. Our approach consists of a plug-in "generator" used to augment the data with an additional class of points that lie on the boundary of the training data, followed by Bayesian inference on top of features that are trained to distinguish these "out-of-distribution" points.

Learned Uncertainty-Aware (LUNA) Bases for Bayesian Regression using Multi-Headed Auxiliary Networks

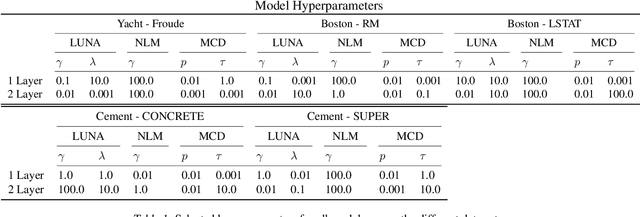
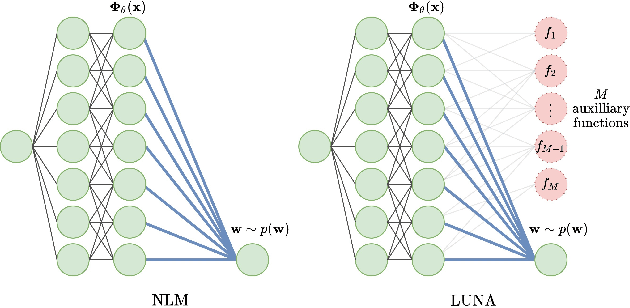
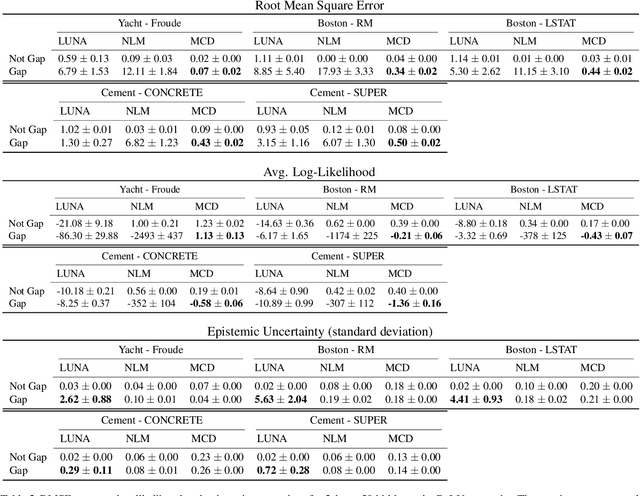
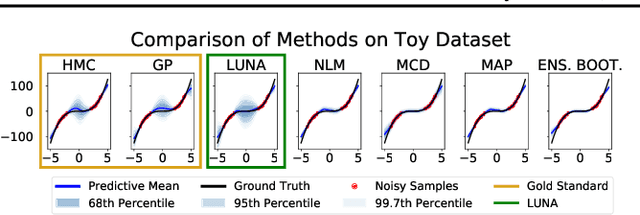
Neural Linear Models (NLM) are deep models that produce predictive uncertainty by learning features from the data and then performing Bayesian linear regression over these features. Despite their popularity, few works have focused on formally evaluating the predictive uncertainties of these models. In this work, we show that traditional training procedures for NLMs can drastically underestimate uncertainty in data-scarce regions. We identify the underlying reasons for this behavior and propose a novel training procedure for capturing useful predictive uncertainties.

Characterizing and Avoiding Problematic Global Optima of Variational Autoencoders

Variational Auto-encoders (VAEs) are deep generative latent variable models consisting of two components: a generative model that captures a data distribution p(x) by transforming a distribution p(z) over latent space, and an inference model that infers likely latent codes for each data point (Kingma and Welling, 2013). Recent work shows that traditional training methods tend to yield solutions that violate modeling desiderata: (1) the learned generative model captures the observed data distribution but does so while ignoring the latent codes, resulting in codes that do not represent the data (e.g. van den Oord et al. (2017); Kim et al. (2018)); (2) the aggregate of the learned latent codes does not match the prior p(z). This mismatch means that the learned generative model will be unable to generate realistic data with samples from p(z)(e.g. Makhzani et al. (2015); Tomczak and Welling (2017)). In this paper, we demonstrate that both issues stem from the fact that the global optima of the VAE training objective often correspond to undesirable solutions. Our analysis builds on two observations: (1) the generative model is unidentifiable - there exist many generative models that explain the data equally well, each with different (and potentially unwanted) properties and (2) bias in the VAE objective - the VAE objective may prefer generative models that explain the data poorly but have posteriors that are easy to approximate. We present a novel inference method, LiBI, mitigating the problems identified in our analysis. On synthetic datasets, we show that LiBI can learn generative models that capture the data distribution and inference models that better satisfy modeling assumptions when traditional methods struggle to do so.

Learning Deep Bayesian Latent Variable Regression Models that Generalize: When Non-identifiability is a Problem

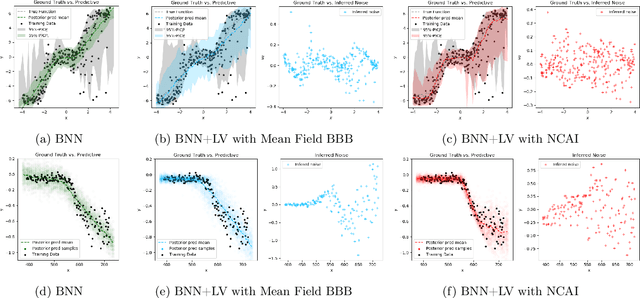
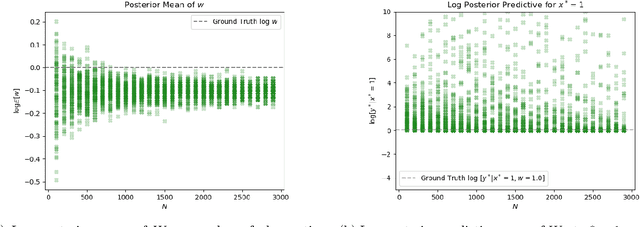
Bayesian Neural Networks with Latent Variables (BNN+LV's) provide uncertainties in prediction estimates by explicitly modeling model uncertainty (via priors on network weights) and environmental stochasticity (via a latent input noise variable). In this work, we first show that BNN+LV suffers from a serious form of non-identifiability: explanatory power can be transferred between model parameters and input noise while fitting the data equally well. We demonstrate that, as a result, traditional inference methods may yield parameters that reconstruct observed data well but generalize poorly. Next, we develop a novel inference procedure that explicitly mitigates the effects of likelihood non-identifiability during training and yields high quality predictions as well as uncertainty estimates. We demonstrate that our inference method improves upon benchmark methods across a range of synthetic and real datasets.