Learning Deep Bayesian Latent Variable Regression Models that Generalize: When Non-identifiability is a Problem
Paper and Code
Nov 01, 2019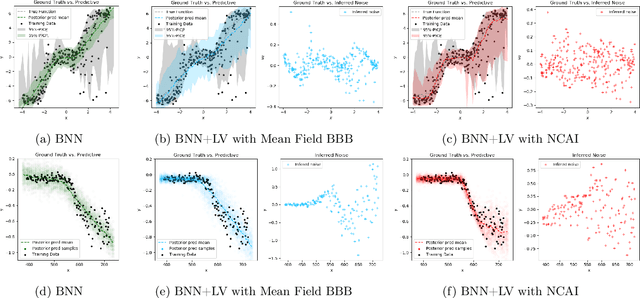

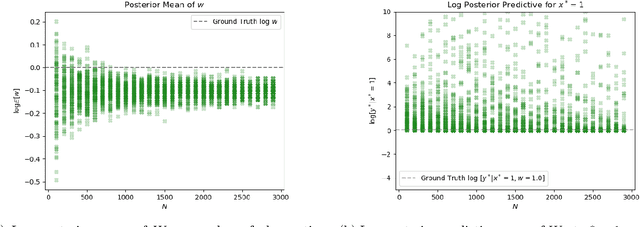

Bayesian Neural Networks with Latent Variables (BNN+LV's) provide uncertainties in prediction estimates by explicitly modeling model uncertainty (via priors on network weights) and environmental stochasticity (via a latent input noise variable). In this work, we first show that BNN+LV suffers from a serious form of non-identifiability: explanatory power can be transferred between model parameters and input noise while fitting the data equally well. We demonstrate that, as a result, traditional inference methods may yield parameters that reconstruct observed data well but generalize poorly. Next, we develop a novel inference procedure that explicitly mitigates the effects of likelihood non-identifiability during training and yields high quality predictions as well as uncertainty estimates. We demonstrate that our inference method improves upon benchmark methods across a range of synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge