Dissecting Medical Referral Mechanisms in Health Services: Role of Physician Professional Networks

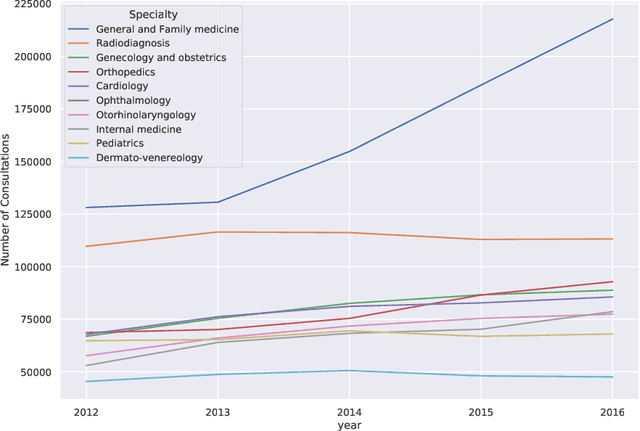
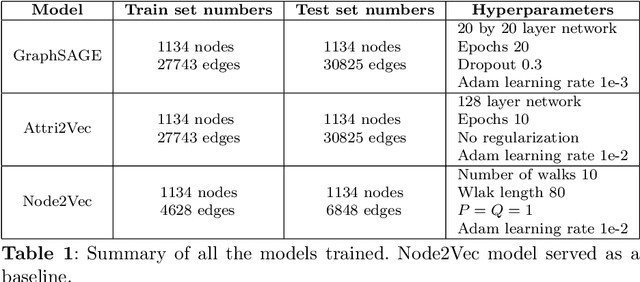
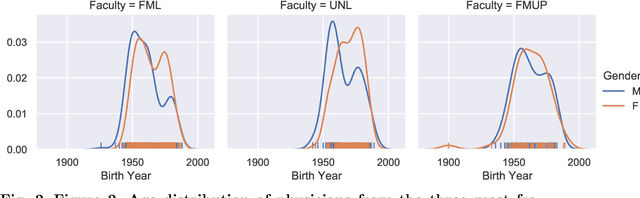
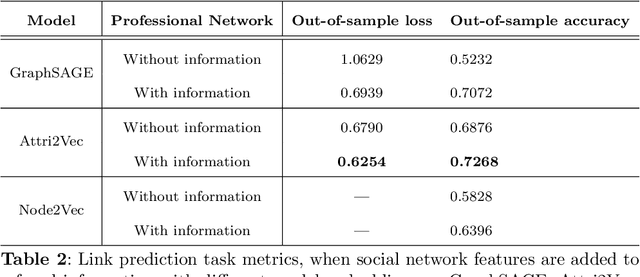
Medical referrals between primary care physicians (PC) and specialist care (SC) physicians profoundly impact patient care regarding quality, satisfaction, and cost. This paper investigates the influence of professional networks among medical doctors on referring patients from PC to SC. Using five-year consultation data from a Portuguese private health provider, we conducted exploratory data analysis and constructed both professional and referral networks among physicians. We then apply Graph Neural Network (GNN) models to learn latent representations of the referral network. Our analysis supports the hypothesis that doctors' professional social connections can predict medical referrals, potentially enhancing collaboration within organizations and improving healthcare services. This research contributes to dissecting the underlying mechanisms in primary-specialty referrals, thereby providing valuable insights for enhancing patient care and effective healthcare management.

ISEE.U: Distributed online active target localization with unpredictable targets

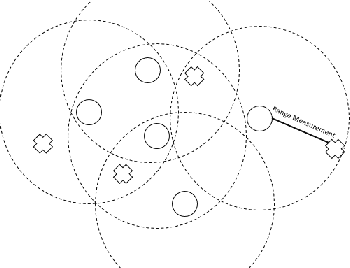
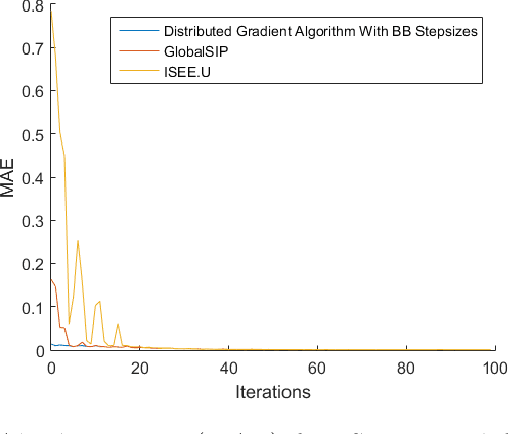
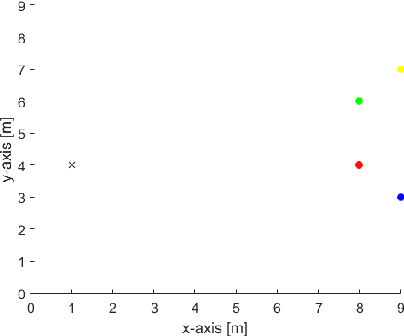
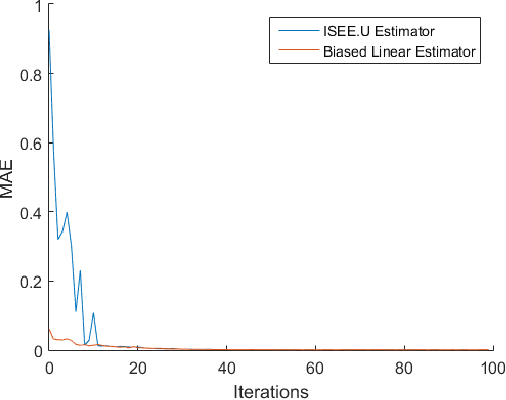
This paper addresses target localization with an online active learning algorithm defined by distributed, simple and fast computations at each node, with no parameters to tune and where the estimate of the target position at each agent is asymptotically equal in expectation to the centralized maximum-likelihood estimator. ISEE.U takes noisy distances at each agent and finds a control that maximizes localization accuracy. We do not assume specific target dynamics and, thus, our method is robust when facing unpredictable targets. Each agent computes the control that maximizes overall target position accuracy via a local estimate of the Fisher Information Matrix. We compared the proposed method with a state of the art algorithm outperforming it when the target movements do not follow a prescribed trajectory, with x100 less computation time, even when our method is running in one central CPU.

COSMIC: fast closed-form identification from large-scale data for LTV systems

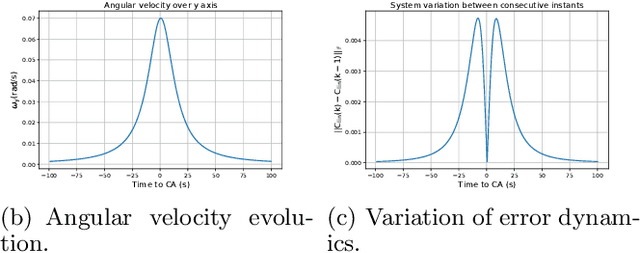
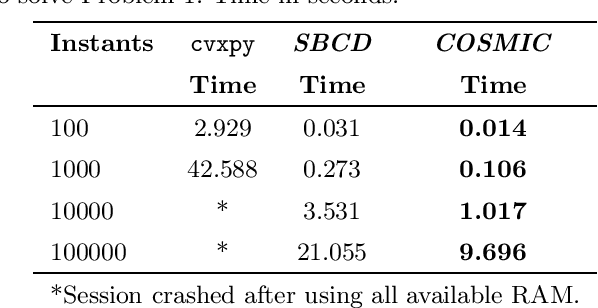
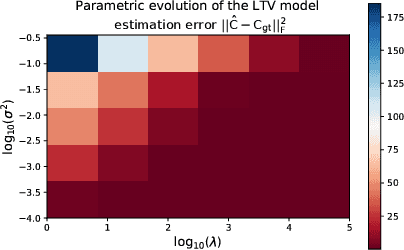
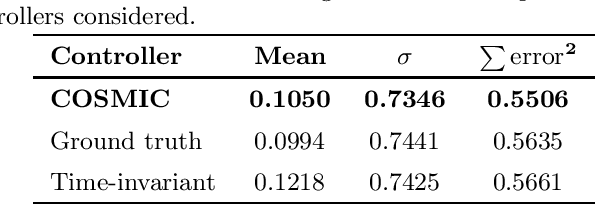
We introduce a closed-form method for identification of discrete-time linear time-variant systems from data, formulating the learning problem as a regularized least squares problem where the regularizer favors smooth solutions within a trajectory. We develop a closed-form algorithm with guarantees of optimality and with a complexity that increases linearly with the number of instants considered per trajectory. The COSMIC algorithm achieves the desired result even in the presence of large volumes of data. Our method solved the problem using two orders of magnitude less computational power than a general purpose convex solver and was about 3 times faster than a Stochastic Block Coordinate Descent especially designed method. Computational times of our method remained in the order of magnitude of the second even for 10k and 100k time instants, where the general purpose solver crashed. To prove its applicability to real world systems, we test with spring-mass-damper system and use the estimated model to find the optimal control path. Our algorithm was applied to both a Low Fidelity and Functional Engineering Simulators for the Comet Interceptor mission, that requires precise pointing of the on-board cameras in a fast dynamics environment. Thus, this paper provides a fast alternative to classical system identification techniques for linear time-variant systems, while proving to be a solid base for applications in the Space industry and a step forward to the incorporation of algorithms that leverage data in such a safety-critical environment.

Decision Support Models for Predicting and Explaining Airport Passenger Connectivity from Data

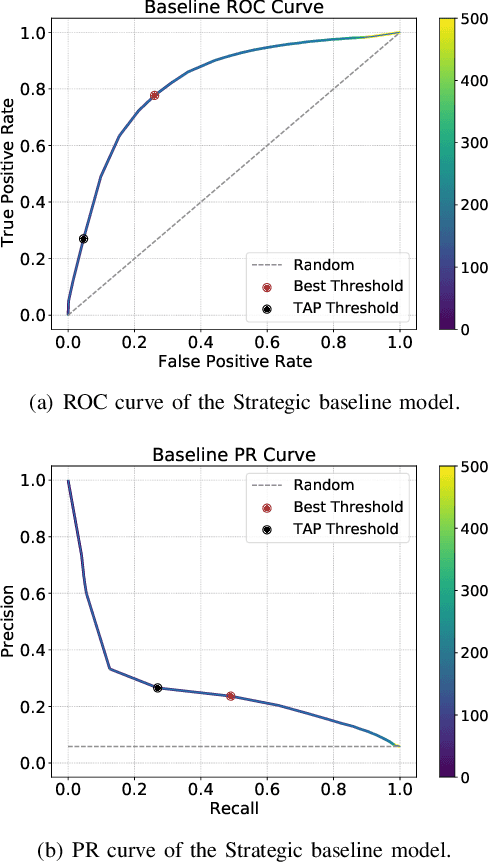
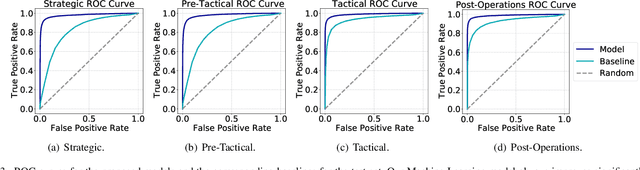
Predicting if passengers in a connecting flight will lose their connection is paramount for airline profitability. We present novel machine learning-based decision support models for the different stages of connection flight management, namely for strategic, pre-tactical, tactical and post-operations. We predict missed flight connections in an airline's hub airport using historical data on flights and passengers, and analyse the factors that contribute additively to the predicted outcome for each decision horizon. Our data is high-dimensional, heterogeneous, imbalanced and noisy, and does not inform about passenger arrival/departure transit time. We employ probabilistic encoding of categorical classes, data balancing with Gaussian Mixture Models, and boosting. For all planning horizons, our models attain an AUC of the ROC higher than 0.93. SHAP value explanations of our models indicate that scheduled/perceived connection times contribute the most to the prediction, followed by passenger age and whether border controls are required.

Range and Bearing Data Fusion for Precise Convex Network Localization

Hybrid localization in GNSS-challenged environments using measured ranges and angles is becoming increasingly popular, in particular with the advent of multimodal communication systems. Here, we address the hybrid network localization problem using ranges and bearings to jointly determine the positions of a number of agents through a single maximum-likelihood (ML) optimization problem that seamlessly fuses all the available pairwise range and angle measurements. We propose a tight convex surrogate to the ML estimator, we examine practical measures for the accuracy of the relaxation, and we comprehensively characterize its behavior in simulation. We found that our relaxation outperforms a state of the art SDP relaxation by one order of magnitude in terms of localization error, and is amenable to much more lightweight solution algorithms.

STRONG: Synchronous and asynchronous RObust Network localization, under Non-Gaussian noise

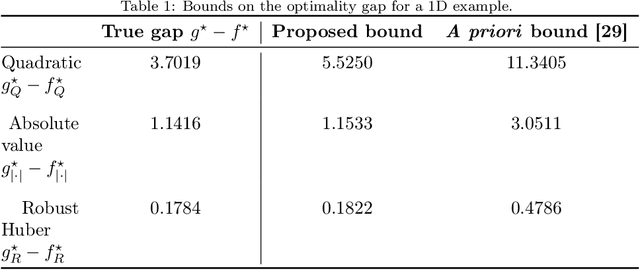
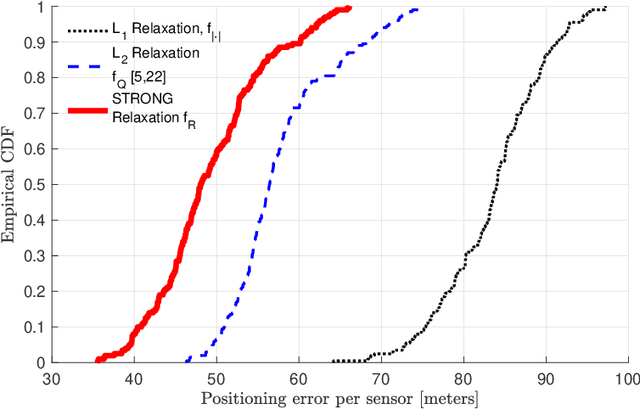
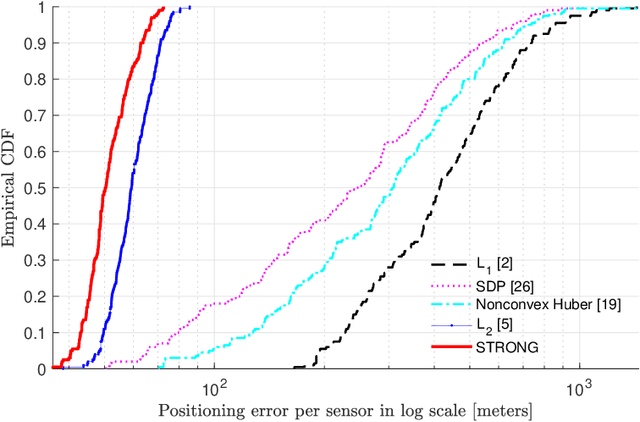
Real-world network applications must cope with failing nodes, malicious attacks, or nodes facing corrupted data - data classified as outliers. Our work addresses these concerns in the scope of the sensor network localization problem where, despite the abundance of technical literature, prior research seldom considered outlier data. We propose robust, fast, and distributed network localization algorithms, resilient to high-power noise, but also precise under regular Gaussian noise. We use a Huber M-estimator, thus obtaining a robust (but nonconvex) optimization problem. We convexify and change the problem representation, to allow for distributed robust localization algorithms: a synchronous distributed method that has optimal convergence rate and an asynchronous one with proven convergence guarantees. A major highlight of our contribution lies on the fact that we pay no price for provable distributed computation neither in accuracy, nor in communication cost or convergence speed. Simulations showcase the superior performance of our algorithms, both in the presence of outliers and under regular Gaussian noise: our method exceeds the accuracy of alternative approaches, distributed and centralized, even under heavy additive and multiplicative outlier noise.

Accurate, Interpretable, and Fast Animation: An Iterative, Sparse, and Nonconvex Approach

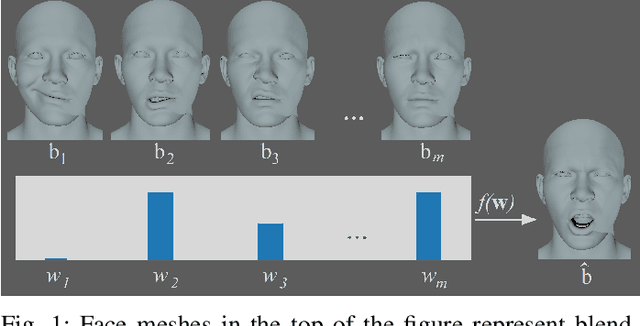
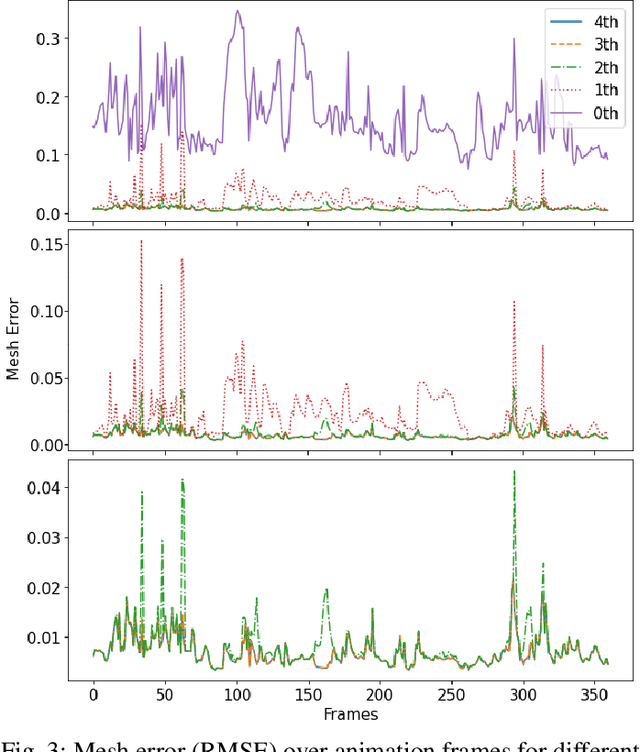
Digital human animation relies on high-quality 3D models of the human face: rigs. A face rig must be accurate and, at the same time, fast to compute. One of the most common rigging models is the blendshape model. We propose a novel algorithm for solving the nonconvex inverse rig problem in facial animation. Our approach is model-based, but in contrast with previous model-based approaches, we use a quadratic instead of the linear approximation to the higher order rig model. This increases the accuracy of the solution by 8 percent on average and, confirmed by the empirical results, increases the sparsity of the resulting parameter vector -- an important feature for interpretability by animation artists. The proposed solution is based on a Levenberg-Marquardt (LM) algorithm, applied to a nonconvex constrained problem with sparsity regularization. In order to reduce the complexity of the iterates, a paradigm of Majorization Minimization (MM) is further invoked, which leads to an easy to solve problem that is separable in the parameters at each algorithm iteration. The algorithm is evaluated on a number of animation datasets, proprietary and open-source, and the results indicate the superiority of our method compared to the standard approach based on the linear rig approximation. Although our algorithm targets the specific problem, it might have additional signal processing applications.

Conjunction Data Messages behave as a Poisson Process

Space debris is a major problem in space exploration. International bodies continuously monitor a large database of orbiting objects and emit warnings in the form of conjunction data messages. An important question for satellite operators is to estimate when fresh information will arrive so that they can react timely but sparingly with satellite maneuvers. We propose a statistical learning model of the message arrival process, allowing us to answer two important questions: (1) Will there be any new message in the next specified time interval? (2) When exactly and with what uncertainty will the next message arrive? The average prediction error for question (2) of our Bayesian Poisson process model is smaller than the baseline in more than 3 hours in a test set of 50k close encounter events.