OrbitZoo: Multi-Agent Reinforcement Learning Environment for Orbital Dynamics

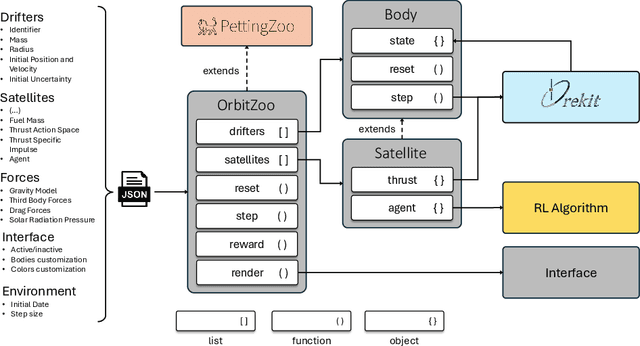
The increasing number of satellites and orbital debris has made space congestion a critical issue, threatening satellite safety and sustainability. Challenges such as collision avoidance, station-keeping, and orbital maneuvering require advanced techniques to handle dynamic uncertainties and multi-agent interactions. Reinforcement learning (RL) has shown promise in this domain, enabling adaptive, autonomous policies for space operations; however, many existing RL frameworks rely on custom-built environments developed from scratch, which often use simplified models and require significant time to implement and validate the orbital dynamics, limiting their ability to fully capture real-world complexities. To address this, we introduce OrbitZoo, a versatile multi-agent RL environment built on a high-fidelity industry standard library, that enables realistic data generation, supports scenarios like collision avoidance and cooperative maneuvers, and ensures robust and accurate orbital dynamics. The environment is validated against a real satellite constellation, Starlink, achieving a Mean Absolute Percentage Error (MAPE) of 0.16% compared to real-world data. This validation ensures reliability for generating high-fidelity simulations and enabling autonomous and independent satellite operations.

Advancing Solutions for the Three-Body Problem Through Physics-Informed Neural Networks

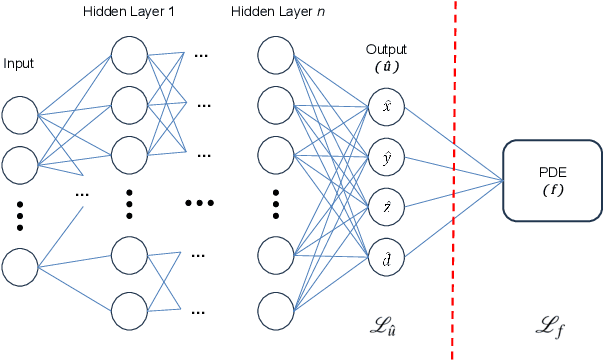
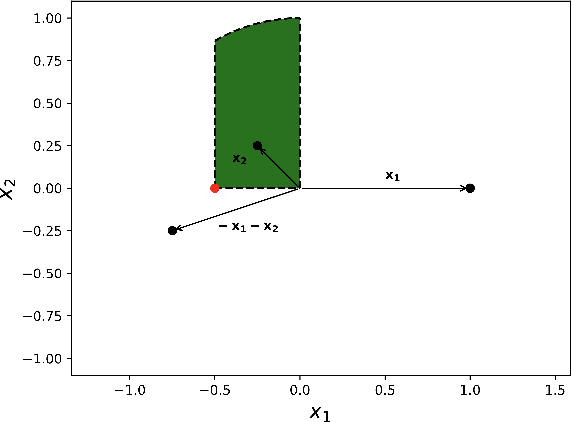
First formulated by Sir Isaac Newton in his work "Philosophiae Naturalis Principia Mathematica", the concept of the Three-Body Problem was put forth as a study of the motion of the three celestial bodies within the Earth-Sun-Moon system. In a generalized definition, it seeks to predict the motion for an isolated system composed of three point masses freely interacting under Newton's law of universal attraction. This proves to be analogous to a multitude of interactions between celestial bodies, and thus, the problem finds applicability within the studies of celestial mechanics. Despite numerous attempts by renowned physicists to solve it throughout the last three centuries, no general closed-form solutions have been reached due to its inherently chaotic nature for most initial conditions. Current state-of-the-art solutions are based on two approaches, either numerical high-precision integration or machine learning-based. Notwithstanding the breakthroughs of neural networks, these present a significant limitation, which is their ignorance of any prior knowledge of the chaotic systems presented. Thus, in this work, we propose a novel method that utilizes Physics-Informed Neural Networks (PINNs). These deep neural networks are able to incorporate any prior system knowledge expressible as an Ordinary Differential Equation (ODE) into their learning processes as a regularizing agent. Our findings showcase that PINNs surpass current state-of-the-art machine learning methods with comparable prediction quality. Despite a better prediction quality, the usability of numerical integrators suffers due to their prohibitively high computational cost. These findings confirm that PINNs are both effective and time-efficient open-form solvers of the Three-Body Problem that capitalize on the extensive knowledge we hold of classical mechanics.

Conjunction Data Messages for Space Collision Behave as a Poisson Process

Space debris is a major problem in space exploration. International bodies continuously monitor a large database of orbiting objects and emit warnings in the form of conjunction data messages. An important question for satellite operators is to estimate when fresh information will arrive so that they can react timely but sparingly with satellite maneuvers. We propose a statistical learning model of the message arrival process, allowing us to answer two important questions: (1) Will there be any new message in the next specified time interval? (2) When exactly and with what uncertainty will the next message arrive? The average prediction error for question (2) of our Bayesian Poisson process model is smaller than the baseline in more than 4 hours in a test set of 50k close encounter events.

Machine Learning in Orbit Estimation: a Survey

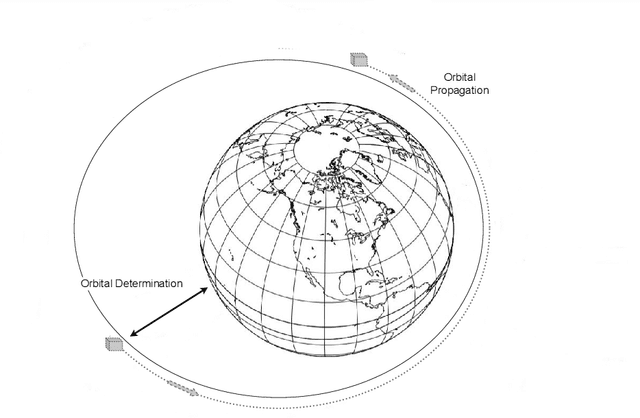
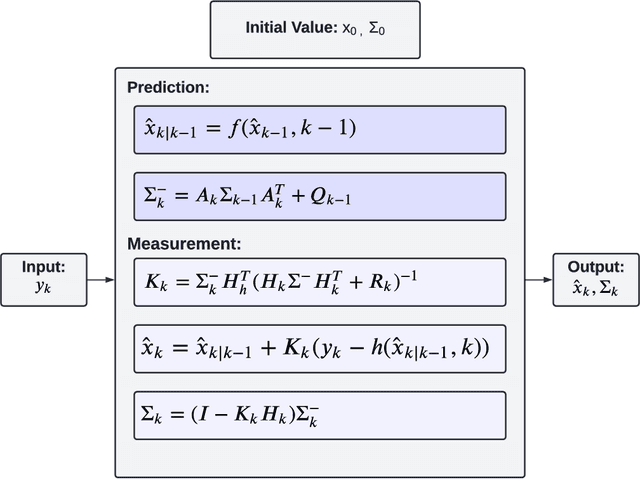
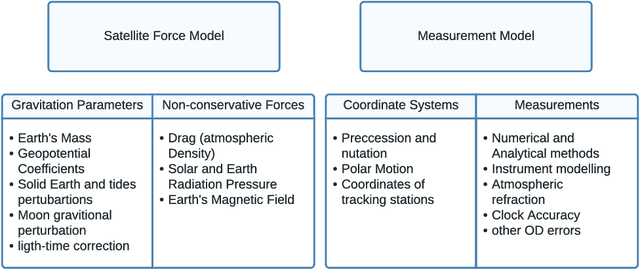
Since the late '50s, when the first artificial satellite was launched, the number of resident space objects (RSOs) has steadily increased. It is estimated that around 1 Million objects larger than 1 cm are currently orbiting the Earth, with only 30,000, larger than 10 cm, presently being tracked. To avert a chain reaction of collisions, termed Kessler Syndrome, it is indispensable to accurately track and predict space debris and satellites' orbit alike. Current physics-based methods have errors in the order of kilometres for 7 days predictions, which is insufficient when considering space debris that have mostly less than 1 meter. Typically, this failure is due to uncertainty around the state of the space object at the beginning of the trajectory, forecasting errors in environmental conditions such as atmospheric drag, as well as specific unknown characteristics such as mass or geometry of the RSO. Leveraging data-driven techniques, namely machine learning, the orbit prediction accuracy can be enhanced: by deriving unmeasured objects' characteristics, improving non-conservative forces' effects, and by the superior abstraction capacity that Deep Learning models have of modelling highly complex non-linear systems. In this survey, we provide an overview of the current work being done in this field.

Conjunction Data Messages behave as a Poisson Process

Space debris is a major problem in space exploration. International bodies continuously monitor a large database of orbiting objects and emit warnings in the form of conjunction data messages. An important question for satellite operators is to estimate when fresh information will arrive so that they can react timely but sparingly with satellite maneuvers. We propose a statistical learning model of the message arrival process, allowing us to answer two important questions: (1) Will there be any new message in the next specified time interval? (2) When exactly and with what uncertainty will the next message arrive? The average prediction error for question (2) of our Bayesian Poisson process model is smaller than the baseline in more than 3 hours in a test set of 50k close encounter events.