Luís Tripa
Advancing Solutions for the Three-Body Problem Through Physics-Informed Neural Networks
Mar 06, 2025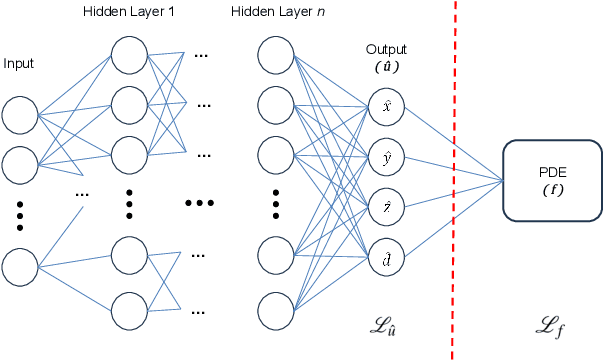


Abstract:First formulated by Sir Isaac Newton in his work "Philosophiae Naturalis Principia Mathematica", the concept of the Three-Body Problem was put forth as a study of the motion of the three celestial bodies within the Earth-Sun-Moon system. In a generalized definition, it seeks to predict the motion for an isolated system composed of three point masses freely interacting under Newton's law of universal attraction. This proves to be analogous to a multitude of interactions between celestial bodies, and thus, the problem finds applicability within the studies of celestial mechanics. Despite numerous attempts by renowned physicists to solve it throughout the last three centuries, no general closed-form solutions have been reached due to its inherently chaotic nature for most initial conditions. Current state-of-the-art solutions are based on two approaches, either numerical high-precision integration or machine learning-based. Notwithstanding the breakthroughs of neural networks, these present a significant limitation, which is their ignorance of any prior knowledge of the chaotic systems presented. Thus, in this work, we propose a novel method that utilizes Physics-Informed Neural Networks (PINNs). These deep neural networks are able to incorporate any prior system knowledge expressible as an Ordinary Differential Equation (ODE) into their learning processes as a regularizing agent. Our findings showcase that PINNs surpass current state-of-the-art machine learning methods with comparable prediction quality. Despite a better prediction quality, the usability of numerical integrators suffers due to their prohibitively high computational cost. These findings confirm that PINNs are both effective and time-efficient open-form solvers of the Three-Body Problem that capitalize on the extensive knowledge we hold of classical mechanics.
* 14 pages, 25 figures, 3 tables. 75th International Astronautical Congress (IAC), Milan, Italy, 14-18 October
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge