Maria Carvalho
Deep Aesthetic Assessment and Retrieval of Breast Cancer Treatment Outcomes
May 25, 2022Abstract:Treatments for breast cancer have continued to evolve and improve in recent years, resulting in a substantial increase in survival rates, with approximately 80\% of patients having a 10-year survival period. Given the serious impact that breast cancer treatments can have on a patient's body image, consequently affecting her self-confidence and sexual and intimate relationships, it is paramount to ensure that women receive the treatment that optimizes both survival and aesthetic outcomes. Currently, there is no gold standard for evaluating the aesthetic outcome of breast cancer treatment. In addition, there is no standard way to show patients the potential outcome of surgery. The presentation of similar cases from the past would be extremely important to manage women's expectations of the possible outcome. In this work, we propose a deep neural network to perform the aesthetic evaluation. As a proof-of-concept, we focus on a binary aesthetic evaluation. Besides its use for classification, this deep neural network can also be used to find the most similar past cases by searching for nearest neighbours in the highly semantic space before classification. We performed the experiments on a dataset consisting of 143 photos of women after conservative treatment for breast cancer. The results for accuracy and balanced accuracy showed the superior performance of our proposed model compared to the state of the art in aesthetic evaluation of breast cancer treatments. In addition, the model showed a good ability to retrieve similar previous cases, with the retrieved cases having the same or adjacent class (in the 4-class setting) and having similar types of asymmetry. Finally, a qualitative interpretability assessment was also performed to analyse the robustness and trustworthiness of the model.
COSMIC: fast closed-form identification from large-scale data for LTV systems
Dec 08, 2021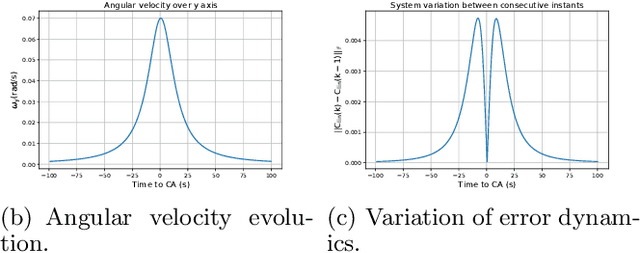
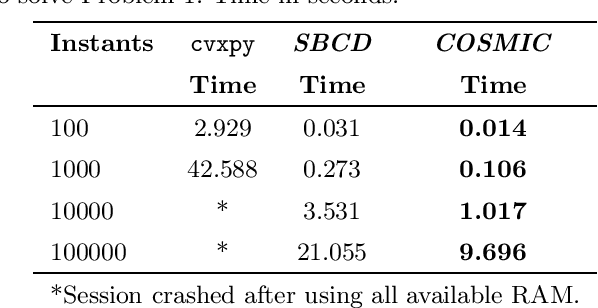
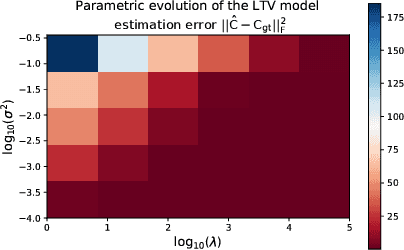
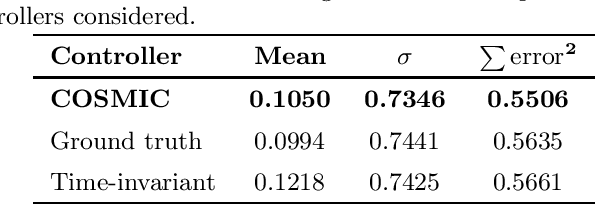
Abstract:We introduce a closed-form method for identification of discrete-time linear time-variant systems from data, formulating the learning problem as a regularized least squares problem where the regularizer favors smooth solutions within a trajectory. We develop a closed-form algorithm with guarantees of optimality and with a complexity that increases linearly with the number of instants considered per trajectory. The COSMIC algorithm achieves the desired result even in the presence of large volumes of data. Our method solved the problem using two orders of magnitude less computational power than a general purpose convex solver and was about 3 times faster than a Stochastic Block Coordinate Descent especially designed method. Computational times of our method remained in the order of magnitude of the second even for 10k and 100k time instants, where the general purpose solver crashed. To prove its applicability to real world systems, we test with spring-mass-damper system and use the estimated model to find the optimal control path. Our algorithm was applied to both a Low Fidelity and Functional Engineering Simulators for the Comet Interceptor mission, that requires precise pointing of the on-board cameras in a fast dynamics environment. Thus, this paper provides a fast alternative to classical system identification techniques for linear time-variant systems, while proving to be a solid base for applications in the Space industry and a step forward to the incorporation of algorithms that leverage data in such a safety-critical environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge