Multi-Scale Label Relation Learning for Multi-Label Classification Using 1-Dimensional Convolutional Neural Networks

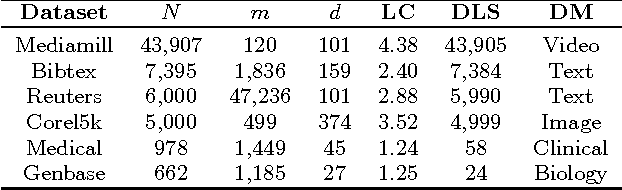
We present Multi-Scale Label Dependence Relation Networks (MSDN), a novel approach to multi-label classification (MLC) using 1-dimensional convolution kernels to learn label dependencies at multi-scale. Modern multi-label classifiers have been adopting recurrent neural networks (RNNs) as a memory structure to capture and exploit label dependency relations. The RNN-based MLC models however tend to introduce a very large number of parameters that may cause under-/over-fitting problems. The proposed method uses the 1-dimensional convolutional neural network (1D-CNN) to serve the same purpose in a more efficient manner. By training a model with multiple kernel sizes, the method is able to learn the dependency relations among labels at multiple scales, while it uses a drastically smaller number of parameters. With public benchmark datasets, we demonstrate that our model can achieve better accuracies with much smaller number of model parameters compared to RNN-based MLC models.

Detection of Abnormal Input-Output Associations

We study a novel outlier detection problem that aims to identify abnormal input-output associations in data, whose instances consist of multi-dimensional input (context) and output (responses) pairs. We present our approach that works by analyzing data in the conditional (input--output) relation space, captured by a decomposable probabilistic model. Experimental results demonstrate the ability of our approach in identifying multivariate conditional outliers.

Detecting Unusual Input-Output Associations in Multivariate Conditional Data

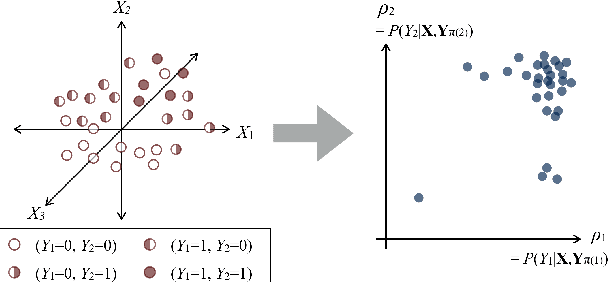
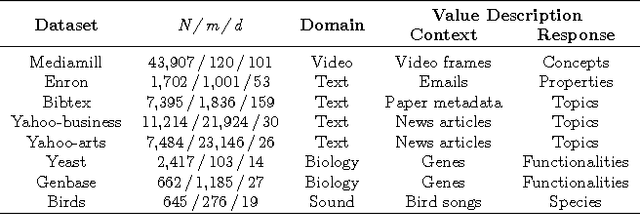
Despite tremendous progress in outlier detection research in recent years, the majority of existing methods are designed only to detect unconditional outliers that correspond to unusual data patterns expressed in the joint space of all data attributes. Such methods are not applicable when we seek to detect conditional outliers that reflect unusual responses associated with a given context or condition. This work focuses on multivariate conditional outlier detection, a special type of the conditional outlier detection problem, where data instances consist of multi-dimensional input (context) and output (responses) pairs. We present a novel outlier detection framework that identifies abnormal input-output associations in data with the help of a decomposable conditional probabilistic model that is learned from all data instances. Since components of this model can vary in their quality, we combine them with the help of weights reflecting their reliability in assessment of outliers. We study two ways of calculating the component weights: global that relies on all data, and local that relies only on instances similar to the target instance. Experimental results on data from various domains demonstrate the ability of our framework to successfully identify multivariate conditional outliers.

Dealing with Class Imbalance using Thresholding

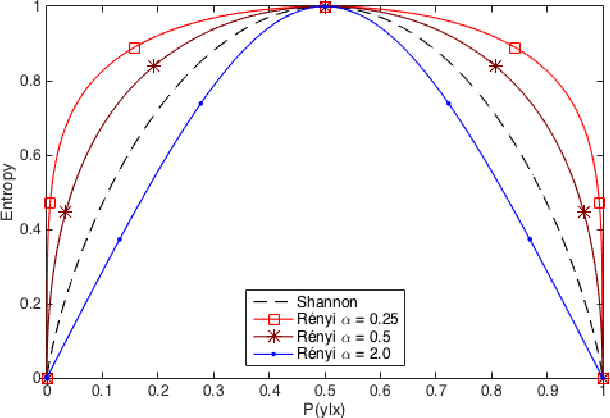
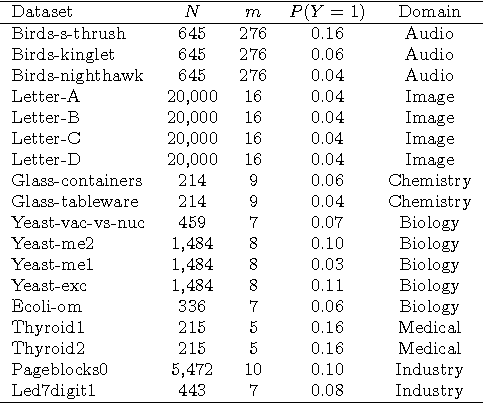
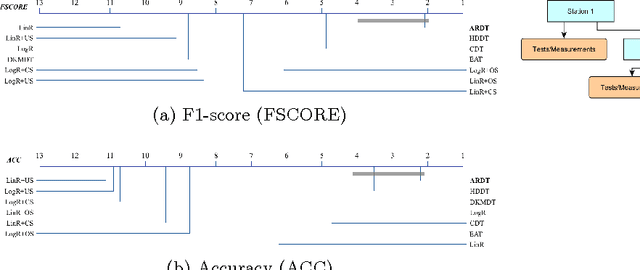
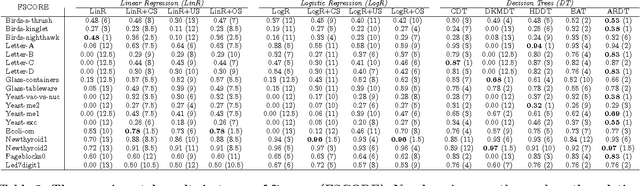
We propose thresholding as an approach to deal with class imbalance. We define the concept of thresholding as a process of determining a decision boundary in the presence of a tunable parameter. The threshold is the maximum value of this tunable parameter where the conditions of a certain decision are satisfied. We show that thresholding is applicable not only for linear classifiers but also for non-linear classifiers. We show that this is the implicit assumption for many approaches to deal with class imbalance in linear classifiers. We then extend this paradigm beyond linear classification and show how non-linear classification can be dealt with under this umbrella framework of thresholding. The proposed method can be used for outlier detection in many real-life scenarios like in manufacturing. In advanced manufacturing units, where the manufacturing process has matured over time, the number of instances (or parts) of the product that need to be rejected (based on a strict regime of quality tests) becomes relatively rare and are defined as outliers. How to detect these rare parts or outliers beforehand? How to detect combination of conditions leading to these outliers? These are the questions motivating our research. This paper focuses on prediction of outliers and conditions leading to outliers using classification. We address the problem of outlier detection using classification. The classes are good parts (those passing the quality tests) and bad parts (those failing the quality tests and can be considered as outliers). The rarity of outliers transforms this problem into a class-imbalanced classification problem.

MCODE: Multivariate Conditional Outlier Detection

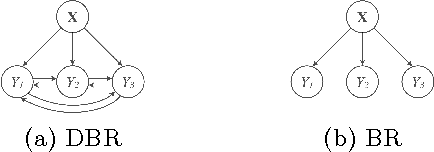
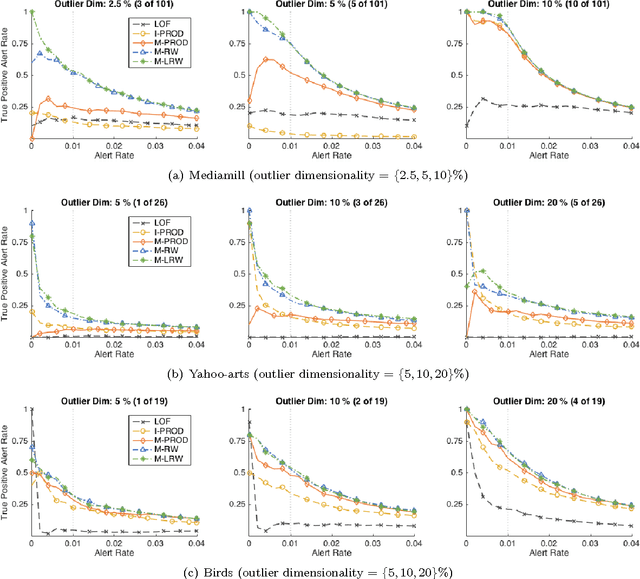
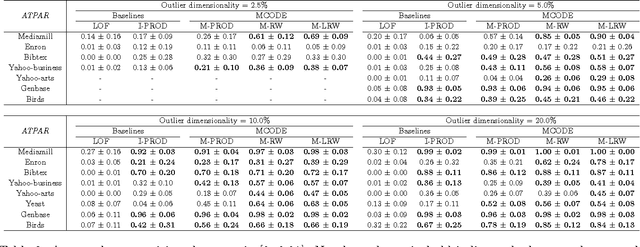
Outlier detection aims to identify unusual data instances that deviate from expected patterns. The outlier detection is particularly challenging when outliers are context dependent and when they are defined by unusual combinations of multiple outcome variable values. In this paper, we develop and study a new conditional outlier detection approach for multivariate outcome spaces that works by (1) transforming the conditional detection to the outlier detection problem in a new (unconditional) space and (2) defining outlier scores by analyzing the data in the new space. Our approach relies on the classifier chain decomposition of the multi-dimensional classification problem that lets us transform the output space into a probability vector, one probability for each dimension of the output space. Outlier scores applied to these transformed vectors are then used to detect the outliers. Experiments on multiple multi-dimensional classification problems with the different outlier injection rates show that our methodology is robust and able to successfully identify outliers when outliers are either sparse (manifested in one or very few dimensions) or dense (affecting multiple dimensions).

A Mixtures-of-Experts Framework for Multi-Label Classification

We develop a novel probabilistic approach for multi-label classification that is based on the mixtures-of-experts architecture combined with recently introduced conditional tree-structured Bayesian networks. Our approach captures different input-output relations from multi-label data using the efficient tree-structured classifiers, while the mixtures-of-experts architecture aims to compensate for the tree-structured restrictions and build a more accurate model. We develop and present algorithms for learning the model from data and for performing multi-label predictions on future data instances. Experiments on multiple benchmark datasets demonstrate that our approach achieves highly competitive results and outperforms the existing state-of-the-art multi-label classification methods.