Dealing with Class Imbalance using Thresholding
Paper and Code
Jul 10, 2016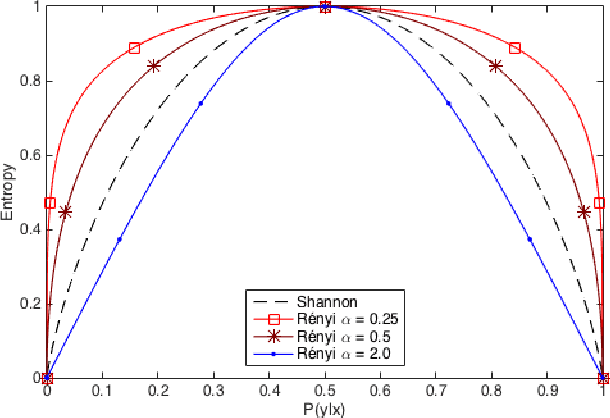
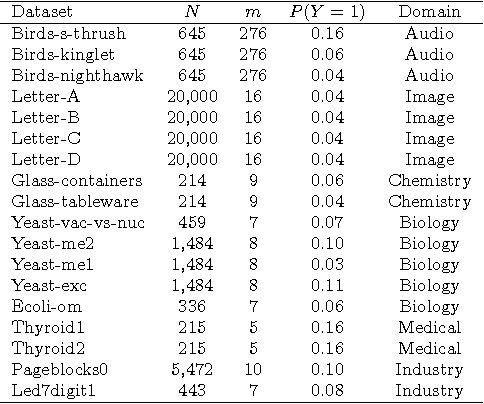
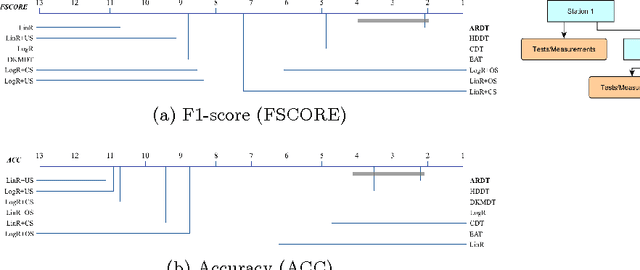
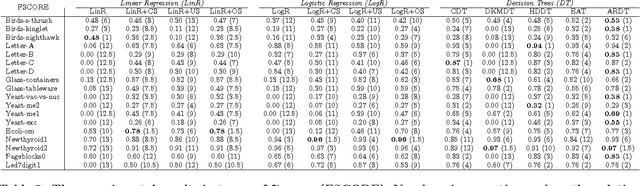
We propose thresholding as an approach to deal with class imbalance. We define the concept of thresholding as a process of determining a decision boundary in the presence of a tunable parameter. The threshold is the maximum value of this tunable parameter where the conditions of a certain decision are satisfied. We show that thresholding is applicable not only for linear classifiers but also for non-linear classifiers. We show that this is the implicit assumption for many approaches to deal with class imbalance in linear classifiers. We then extend this paradigm beyond linear classification and show how non-linear classification can be dealt with under this umbrella framework of thresholding. The proposed method can be used for outlier detection in many real-life scenarios like in manufacturing. In advanced manufacturing units, where the manufacturing process has matured over time, the number of instances (or parts) of the product that need to be rejected (based on a strict regime of quality tests) becomes relatively rare and are defined as outliers. How to detect these rare parts or outliers beforehand? How to detect combination of conditions leading to these outliers? These are the questions motivating our research. This paper focuses on prediction of outliers and conditions leading to outliers using classification. We address the problem of outlier detection using classification. The classes are good parts (those passing the quality tests) and bad parts (those failing the quality tests and can be considered as outliers). The rarity of outliers transforms this problem into a class-imbalanced classification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge