MCODE: Multivariate Conditional Outlier Detection
Paper and Code
May 15, 2015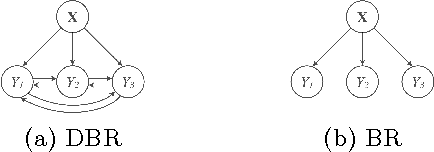

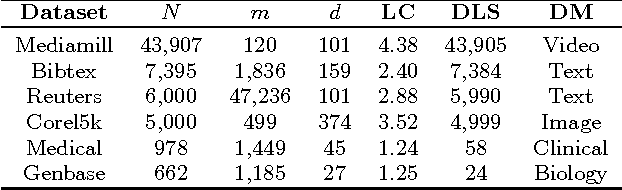

Outlier detection aims to identify unusual data instances that deviate from expected patterns. The outlier detection is particularly challenging when outliers are context dependent and when they are defined by unusual combinations of multiple outcome variable values. In this paper, we develop and study a new conditional outlier detection approach for multivariate outcome spaces that works by (1) transforming the conditional detection to the outlier detection problem in a new (unconditional) space and (2) defining outlier scores by analyzing the data in the new space. Our approach relies on the classifier chain decomposition of the multi-dimensional classification problem that lets us transform the output space into a probability vector, one probability for each dimension of the output space. Outlier scores applied to these transformed vectors are then used to detect the outliers. Experiments on multiple multi-dimensional classification problems with the different outlier injection rates show that our methodology is robust and able to successfully identify outliers when outliers are either sparse (manifested in one or very few dimensions) or dense (affecting multiple dimensions).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge