Property Estimation in Geotechnical Databases Using Labeled Random Finite Sets

The sufficiency of accurate data is a core element in data-centric geotechnics. However, geotechnical datasets are essentially uncertain, whereupon engineers have difficulty with obtaining precise information for making decisions. This challenge is more apparent when the performance of data-driven technologies solely relies on imperfect databases or even when it is sometimes difficult to investigate sites physically. This paper introduces geotechnical property estimation from noisy and incomplete data within the labeled random finite set (LRFS) framework. We leverage the ability of the generalized labeled multi-Bernoulli (GLMB) filter, a fundamental solution for multi-object estimation, to deal with measurement uncertainties from a Bayesian perspective. In particular, this work focuses on the similarity between LRFSs and big indirect data (BID) in geotechnics as those characteristics resemble each other, which enables GLMB filtering to be exploited potentially for data-centric geotechnical engineering. Experiments for numerical study are conducted to evaluate the proposed method using a public clay database.

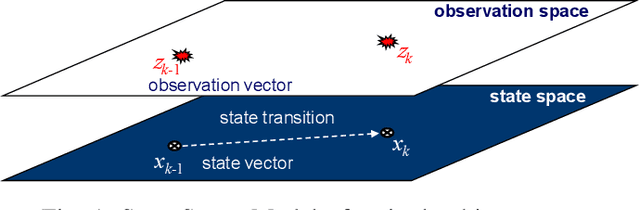
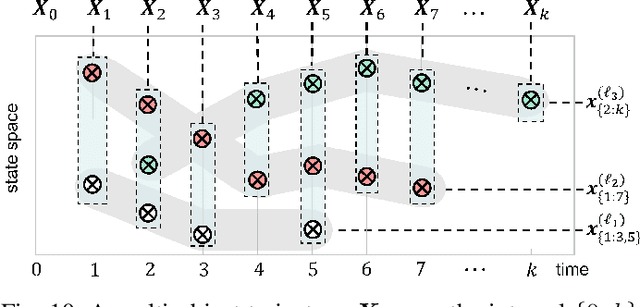
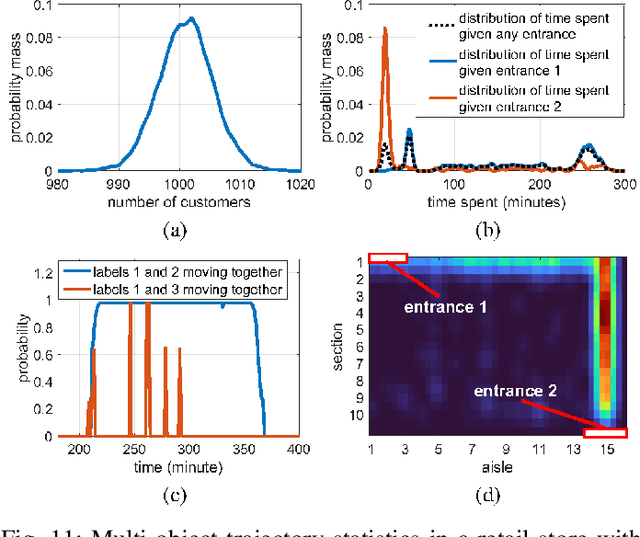
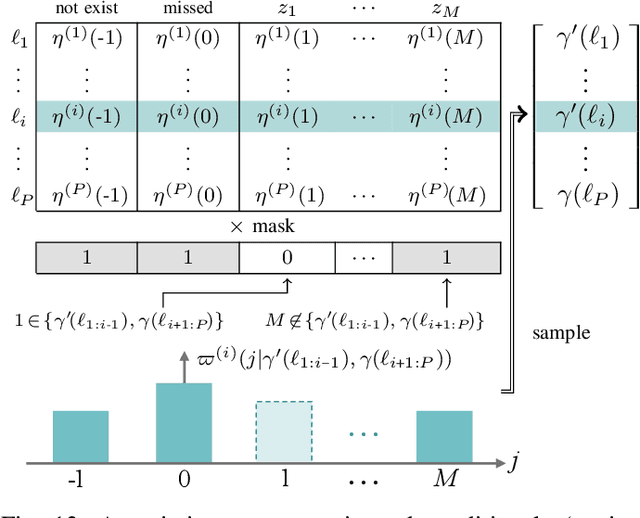
An Overview of Multi-Object Estimation via Labeled Random Finite Set

This article presents the Labeled Random Finite Set (LRFS) framework for multi-object systems-systems in which the number of objects and their states are unknown and vary randomly with time. In particular, we focus on state and trajectory estimation via a multi-object State Space Model (SSM) that admits principled tractable multi-object tracking filters/smoothers. Unlike the single-object counterpart, a time sequence of states does not necessarily represent the trajectory of a multi-object system. The LRFS formulation enables a time sequence of multi-object states to represent the multi-object trajectory that accommodates trajectory crossings and fragmentations. We present the basics of LRFS, covering a suite of commonly used models and mathematical apparatus (including the latest results not published elsewhere). Building on this, we outline the fundamentals of multi-object state space modeling and estimation using LRFS, which formally address object identities/trajectories, ancestries for spawning objects, and characterization of the uncertainty on the ensemble of objects (and their trajectories). Numerical solutions to multi-object SSM problems are inherently far more challenging than those in standard SSM. To bridge the gap between theory and practice, we discuss state-of-the-art implementations that address key computational bottlenecks in the number of objects, measurements, sensors, and scans.

Visual Multi-Object Tracking with Re-Identification and Occlusion Handling using Labeled Random Finite Sets

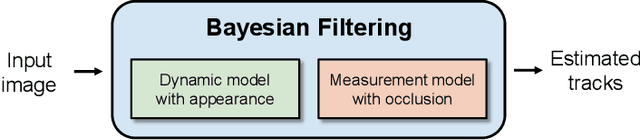
This paper proposes an online visual multi-object tracking (MOT) algorithm that resolves object appearance-reappearance and occlusion. Our solution is based on the labeled random finite set (LRFS) filtering approach, which in principle, addresses disappearance, appearance, reappearance, and occlusion via a single Bayesian recursion. However, in practice, existing numerical approximations cause reappearing objects to be initialized as new tracks, especially after long periods of being undetected. In occlusion handling, the filter's efficacy is dictated by trade-offs between the sophistication of the occlusion model and computational demand. Our contribution is a novel modeling method that exploits object features to address reappearing objects whilst maintaining a linear complexity in the number of detections. Moreover, to improve the filter's occlusion handling, we propose a fuzzy detection model that takes into consideration the overlapping areas between tracks and their sizes. We also develop a fast version of the filter to further reduce the computational time.

The Smooth Trajectory Estimator for LMB Filters

This paper proposes a smooth-trajectory estimator for the labelled multi-Bernoulli (LMB) filter by exploiting the special structure of the generalised labelled multi-Bernoulli (GLMB) filter. We devise a simple and intuitive approach to store the best association map when approximating the GLMB random finite set (RFS) to the LMB RFS. In particular, we construct a smooth-trajectory estimator (i.e., an estimator over the entire trajectories of labelled estimates) for the LMB filter based on the history of the best association map and all of the measurements up to the current time. Experimental results under two challenging scenarios demonstrate significant tracking accuracy improvements with negligible additional computational time compared to the conventional LMB filter. The source code is publicly available at https://tinyurl.com/ste-lmb, aimed at promoting advancements in MOT algorithms.

Label Space Partition Selection for Multi-Object Tracking Using Two-Layer Partitioning

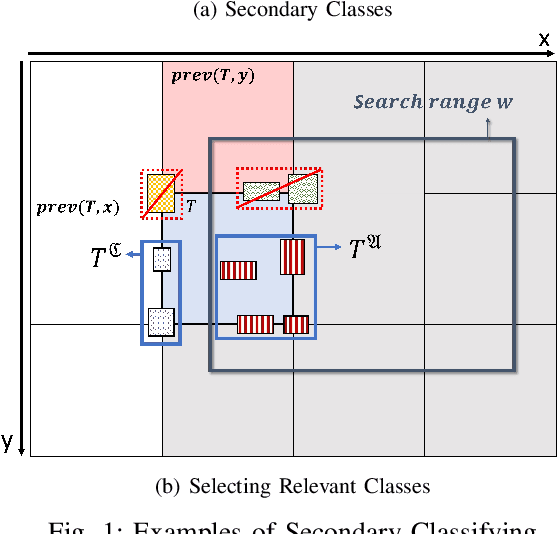
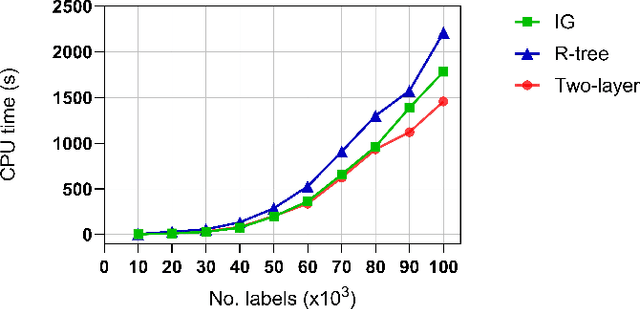
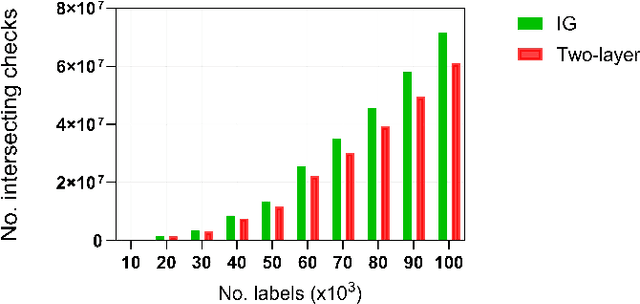
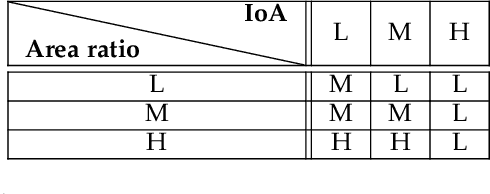
Estimating the trajectories of multi-objects poses a significant challenge due to data association ambiguity, which leads to a substantial increase in computational requirements. To address such problems, a divide-and-conquer manner has been employed with parallel computation. In this strategy, distinguished objects that have unique labels are grouped based on their statistical dependencies, the intersection of predicted measurements. Several geometry approaches have been used for label grouping since finding all intersected label pairs is clearly infeasible for large-scale tracking problems. This paper proposes an efficient implementation of label grouping for label-partitioned generalized labeled multi-Bernoulli filter framework using a secondary partitioning technique. This allows for parallel computation in the label graph indexing step, avoiding generating and eliminating duplicate comparisons. Additionally, we compare the performance of the proposed technique with several efficient spatial searching algorithms. The results demonstrate the superior performance of the proposed approach on large-scale data sets, enabling scalable trajectory estimation.

Linear Complexity Gibbs Sampling for Generalized Labeled Multi-Bernoulli Filtering

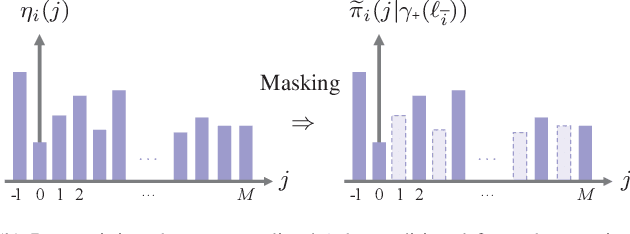
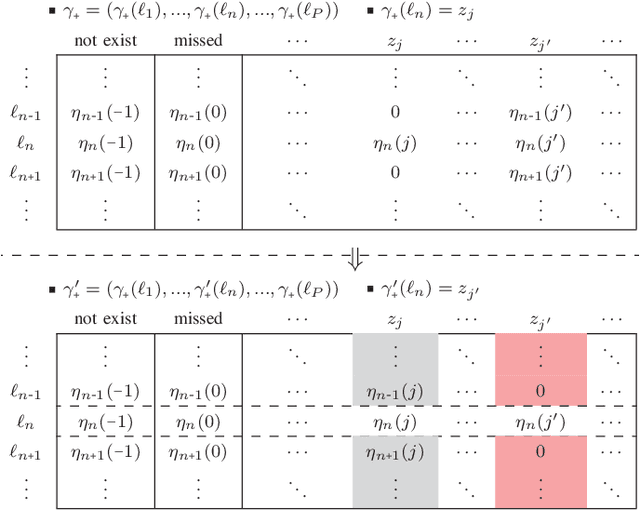
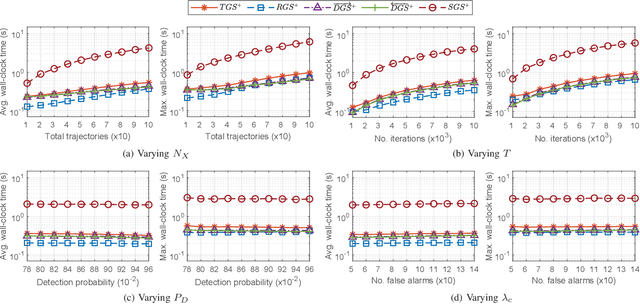
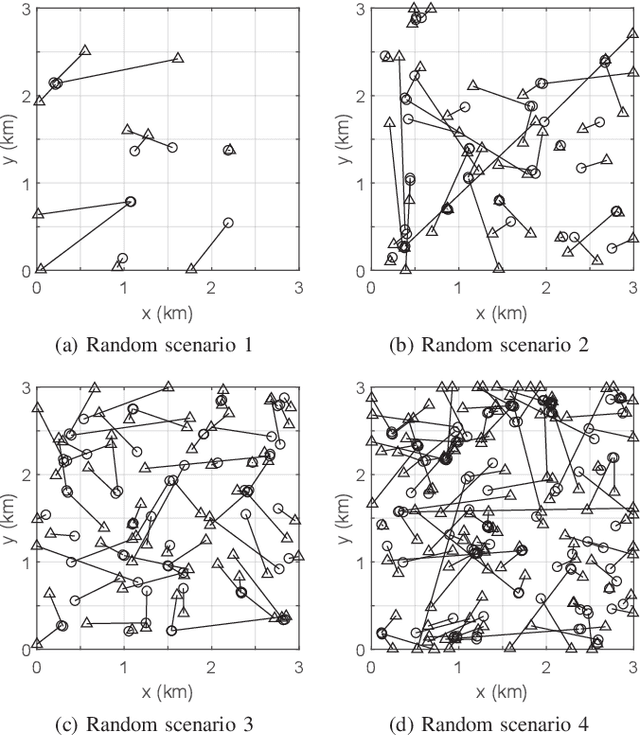
Generalized Labeled Multi-Bernoulli (GLMB) densities arise in a host of multi-object system applications analogous to Gaussians in single-object filtering. However, computing the GLMB filtering density requires solving NP-hard problems. To alleviate this computational bottleneck, we develop a linear complexity Gibbs sampling framework for GLMB density computation. Specifically, we propose a tempered Gibbs sampler that exploits the structure of the GLMB filtering density to achieve an $\mathcal{O}(T(P+M))$ complexity, where $T$ is the number of iterations of the algorithm, $P$ and $M$ are the number hypothesized objects and measurements. This innovation enables an $\mathcal{O}(T(P+M+\log(T))+PM)$ complexity implementation of the GLMB filter. Convergence of the proposed Gibbs sampler is established and numerical studies are presented to validate the proposed GLMB filter implementation.