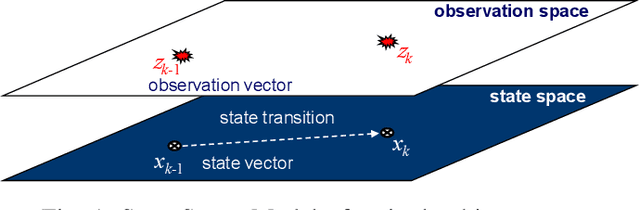
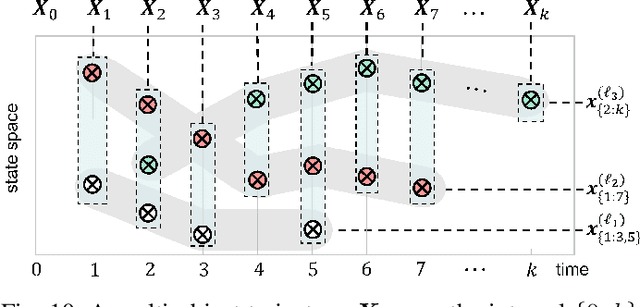
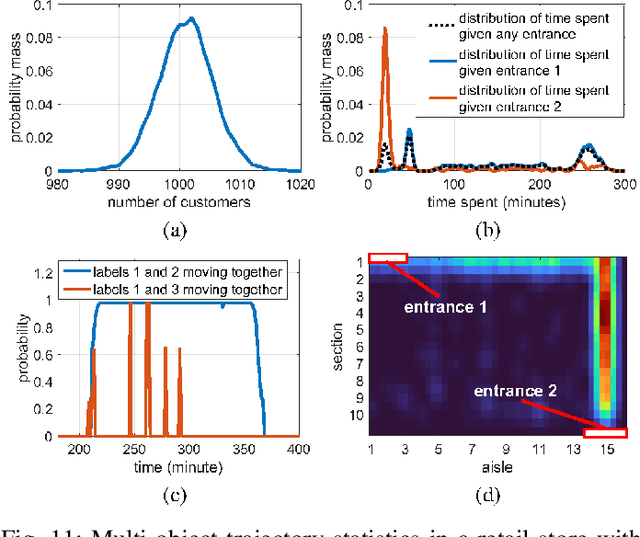
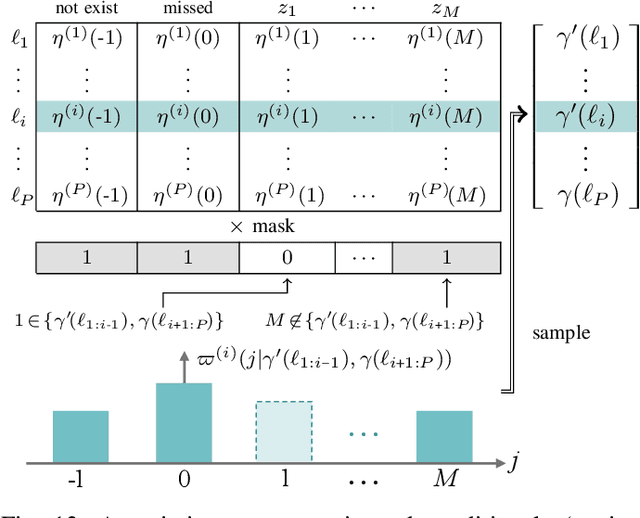
An Overview of Multi-Object Estimation via Labeled Random Finite Set

This article presents the Labeled Random Finite Set (LRFS) framework for multi-object systems-systems in which the number of objects and their states are unknown and vary randomly with time. In particular, we focus on state and trajectory estimation via a multi-object State Space Model (SSM) that admits principled tractable multi-object tracking filters/smoothers. Unlike the single-object counterpart, a time sequence of states does not necessarily represent the trajectory of a multi-object system. The LRFS formulation enables a time sequence of multi-object states to represent the multi-object trajectory that accommodates trajectory crossings and fragmentations. We present the basics of LRFS, covering a suite of commonly used models and mathematical apparatus (including the latest results not published elsewhere). Building on this, we outline the fundamentals of multi-object state space modeling and estimation using LRFS, which formally address object identities/trajectories, ancestries for spawning objects, and characterization of the uncertainty on the ensemble of objects (and their trajectories). Numerical solutions to multi-object SSM problems are inherently far more challenging than those in standard SSM. To bridge the gap between theory and practice, we discuss state-of-the-art implementations that address key computational bottlenecks in the number of objects, measurements, sensors, and scans.

Linear Complexity Gibbs Sampling for Generalized Labeled Multi-Bernoulli Filtering

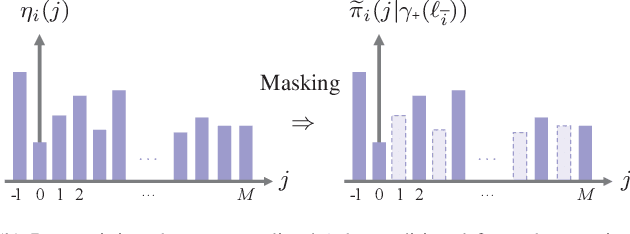
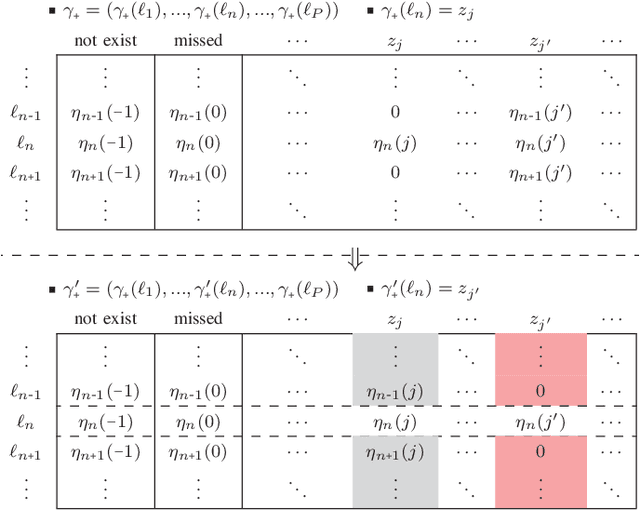
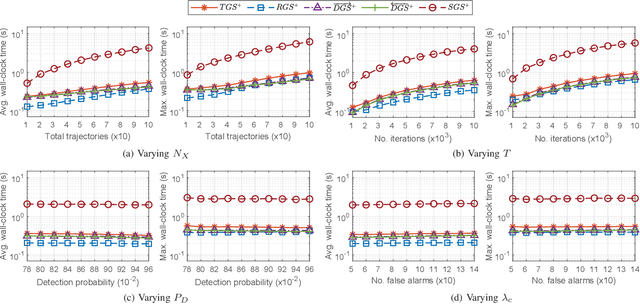
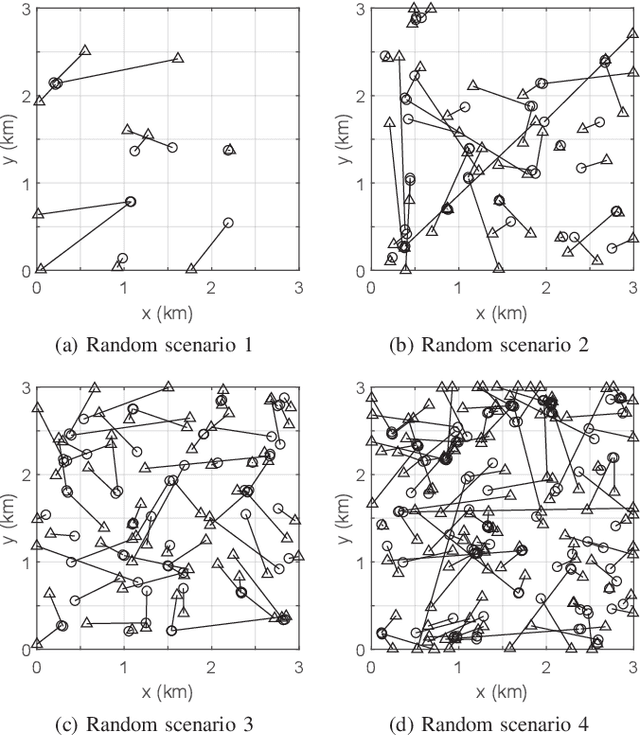
Generalized Labeled Multi-Bernoulli (GLMB) densities arise in a host of multi-object system applications analogous to Gaussians in single-object filtering. However, computing the GLMB filtering density requires solving NP-hard problems. To alleviate this computational bottleneck, we develop a linear complexity Gibbs sampling framework for GLMB density computation. Specifically, we propose a tempered Gibbs sampler that exploits the structure of the GLMB filtering density to achieve an $\mathcal{O}(T(P+M))$ complexity, where $T$ is the number of iterations of the algorithm, $P$ and $M$ are the number hypothesized objects and measurements. This innovation enables an $\mathcal{O}(T(P+M+\log(T))+PM)$ complexity implementation of the GLMB filter. Convergence of the proposed Gibbs sampler is established and numerical studies are presented to validate the proposed GLMB filter implementation.

Tracking Cells and their Lineages via Labeled Random Finite Sets

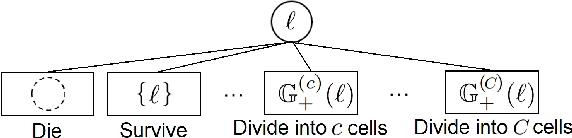
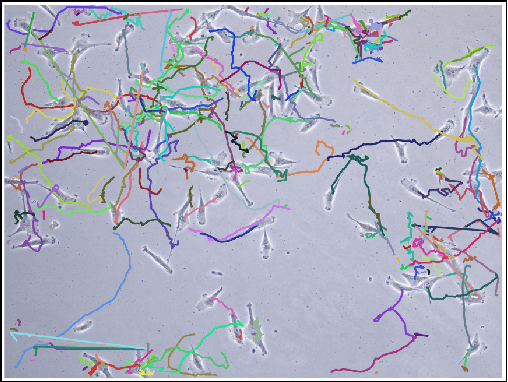
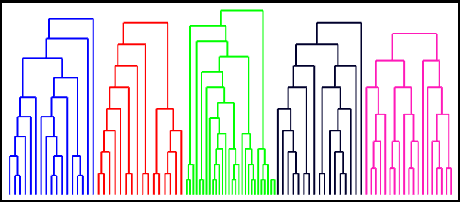
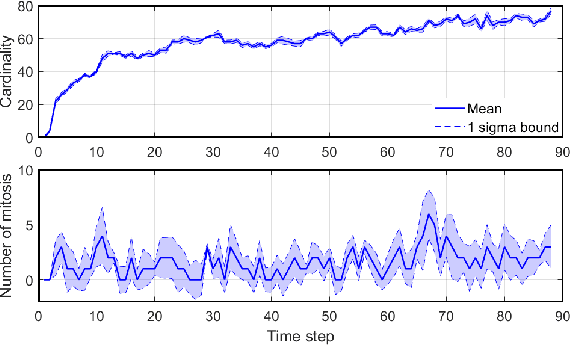
Determining the trajectories of cells and their lineages or ancestries in live-cell experiments are fundamental to the understanding of how cells behave and divide. This paper proposes novel online algorithms for jointly tracking and resolving lineages of an unknown and time-varying number of cells from time-lapse video data. Our approach involves modeling the cell ensemble as a labeled random finite set with labels representing cell identities and lineages. A spawning model is developed to take into account cell lineages and changes in cell appearance prior to division. We then derive analytic filters to propagate multi-object distributions that contain information on the current cell ensemble including their lineages. We also develop numerical implementations of the resulting multi-object filters. Experiments using simulation, synthetic cell migration video, and real time-lapse sequence, are presented to demonstrate the capability of the solutions.

How Trustworthy are the Existing Performance Evaluations for Basic Vision Tasks?

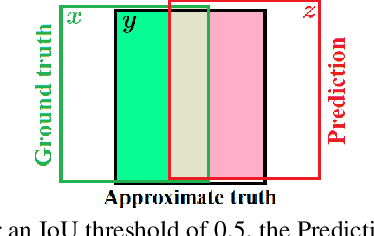
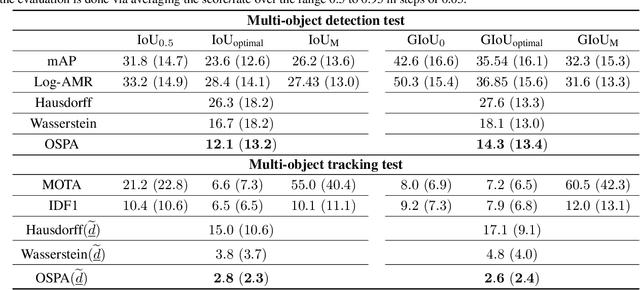
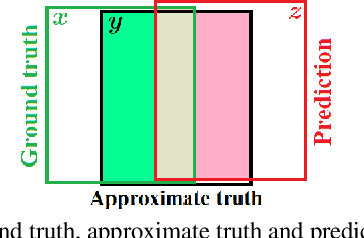
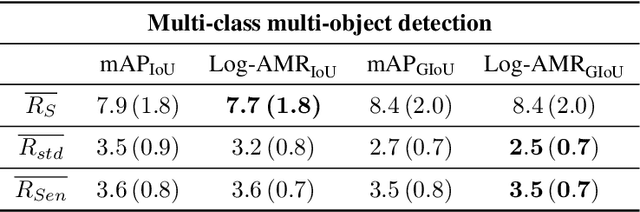
Performance evaluation is indispensable to the advancement of machine vision, yet its consistency and rigour have not received proportionate attention. This paper examines performance evaluation criteria for basic vision tasks namely, object detection, instance-level segmentation and multi-object tracking. Specifically, we advocate the use of criteria that are (i) consistent with mathematical requirements such as the metric properties, (ii) contextually meaningful in sanity tests, and (iii) robust to hyper-parameters for reliability. We show that many widely used performance criteria do not fulfill these requirements. Moreover, we explore alternative criteria for detection, segmentation, and tracking, using metrics for sets of shapes, and assess them against these requirements.

Model-Based Multiple Instance Learning

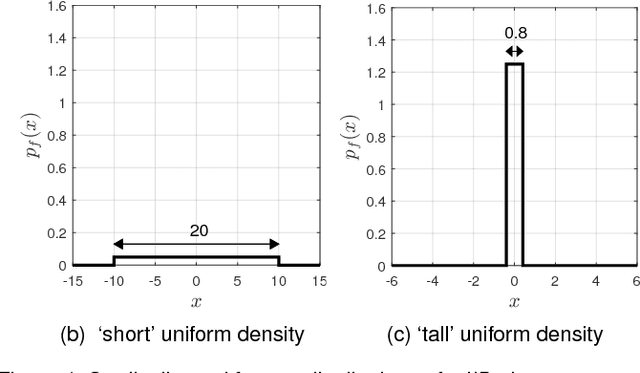
While Multiple Instance (MI) data are point patterns -- sets or multi-sets of unordered points -- appropriate statistical point pattern models have not been used in MI learning. This article proposes a framework for model-based MI learning using point process theory. Likelihood functions for point pattern data derived from point process theory enable principled yet conceptually transparent extensions of learning tasks, such as classification, novelty detection and clustering, to point pattern data. Furthermore, tractable point pattern models as well as solutions for learning and decision making from point pattern data are developed.

Online Visual Multi-Object Tracking via Labeled Random Finite Set Filtering

This paper proposes an online visual multi-object tracking algorithm using a top-down Bayesian formulation that seamlessly integrates state estimation, track management, clutter rejection, occlusion and mis-detection handling into a single recursion. This is achieved by modeling the multi-object state as labeled random finite set and using the Bayes recursion to propagate the multi-object filtering density forward in time. The proposed filter updates tracks with detections but switches to image data when mis-detection occurs, thereby exploiting the efficiency of detection data and the accuracy of image data. Furthermore the labeled random finite set framework enables the incorporation of prior knowledge that mis-detections of long tracks which occur in the middle of the scene are likely to be due to occlusions. Such prior knowledge can be exploited to improve occlusion handling, especially long occlusions that can lead to premature track termination in on-line multi-object tracking. Tracking performance are compared to state-of-the-art algorithms on well-known benchmark video datasets.

Multiple Instance Learning with the Optimal Sub-Pattern Assignment Metric

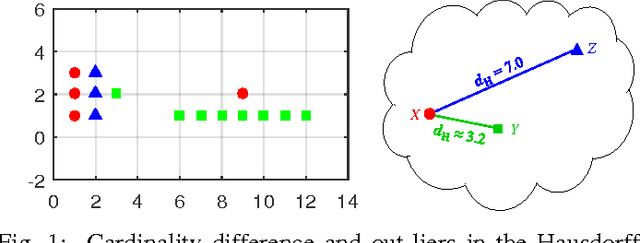
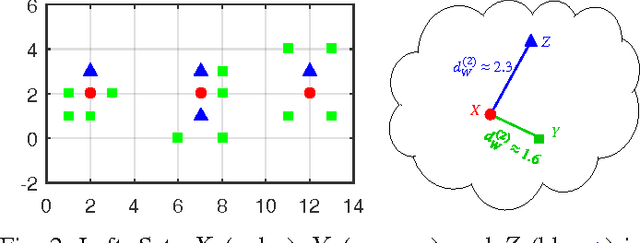
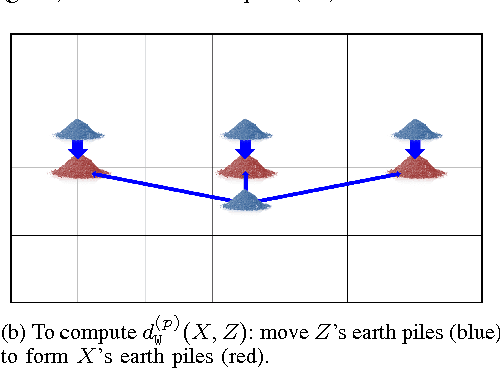
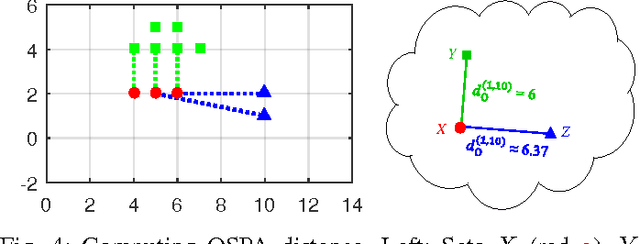
Multiple instance data are sets or multi-sets of unordered elements. Using metrics or distances for sets, we propose an approach to several multiple instance learning tasks, such as clustering (unsupervised learning), classification (supervised learning), and novelty detection (semi-supervised learning). In particular, we introduce the Optimal Sub-Pattern Assignment metric to multiple instance learning so as to provide versatile design choices. Numerical experiments on both simulated and real data are presented to illustrate the versatility of the proposed solution.

Model-based Classification and Novelty Detection For Point Pattern Data

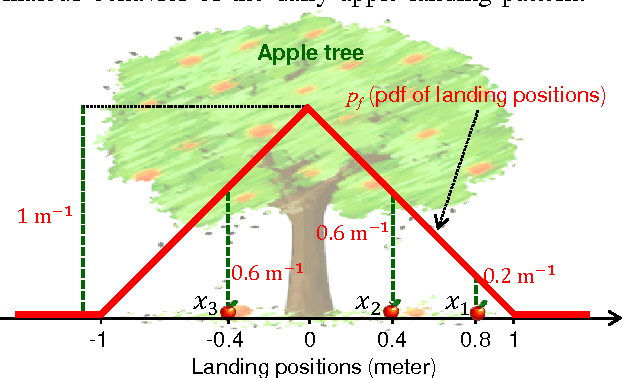
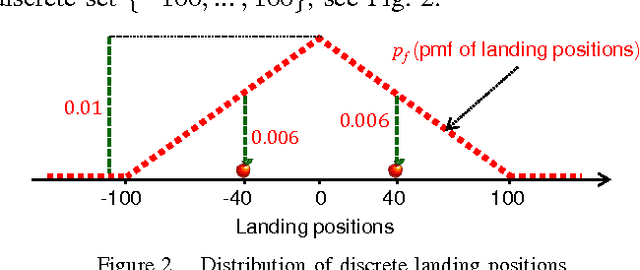
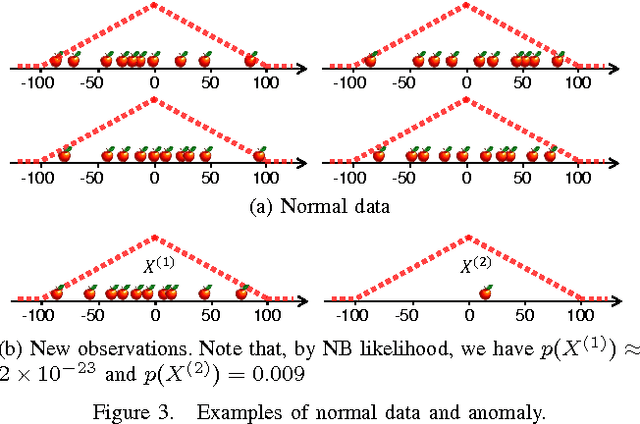
Point patterns are sets or multi-sets of unordered elements that can be found in numerous data sources. However, in data analysis tasks such as classification and novelty detection, appropriate statistical models for point pattern data have not received much attention. This paper proposes the modelling of point pattern data via random finite sets (RFS). In particular, we propose appropriate likelihood functions, and a maximum likelihood estimator for learning a tractable family of RFS models. In novelty detection, we propose novel ranking functions based on RFS models, which substantially improve performance.

Clustering For Point Pattern Data

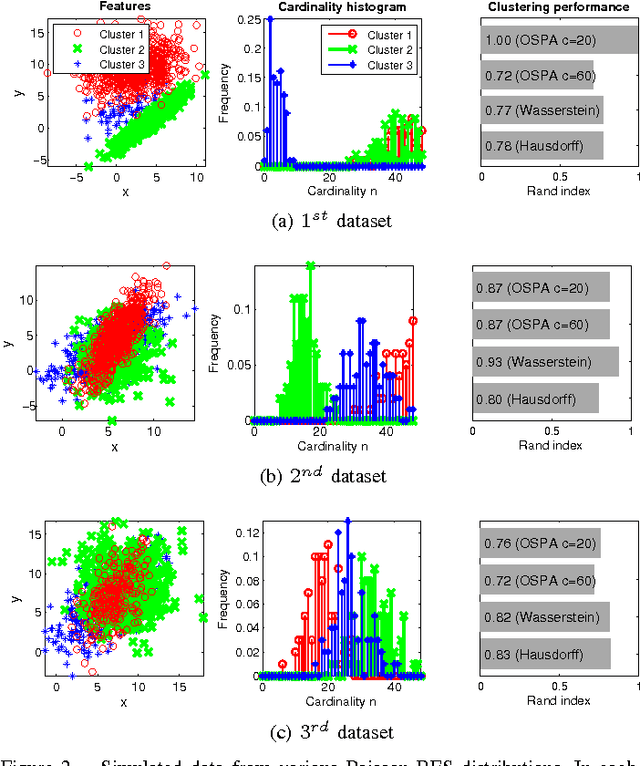
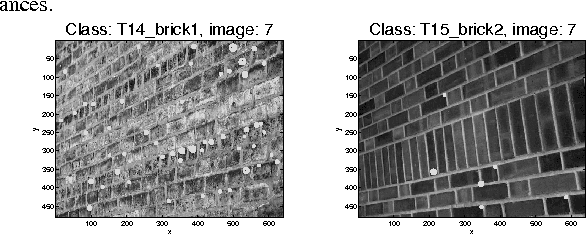
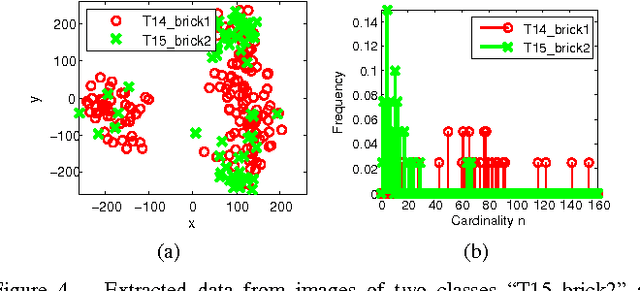
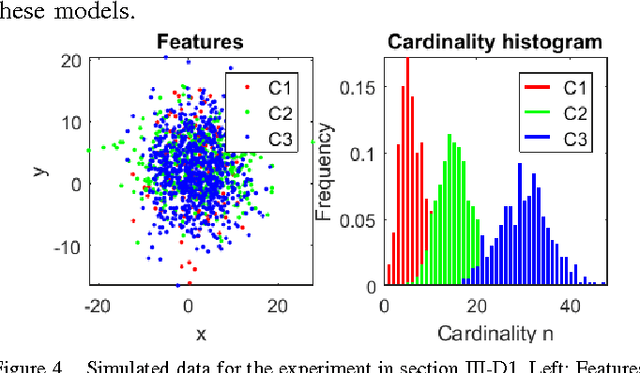
Clustering is one of the most common unsupervised learning tasks in machine learning and data mining. Clustering algorithms have been used in a plethora of applications across several scientific fields. However, there has been limited research in the clustering of point patterns - sets or multi-sets of unordered elements - that are found in numerous applications and data sources. In this paper, we propose two approaches for clustering point patterns. The first is a non-parametric method based on novel distances for sets. The second is a model-based approach, formulated via random finite set theory, and solved by the Expectation-Maximization algorithm. Numerical experiments show that the proposed methods perform well on both simulated and real data.

A Generalized Labeled Multi-Bernoulli Filter Implementation using Gibbs Sampling

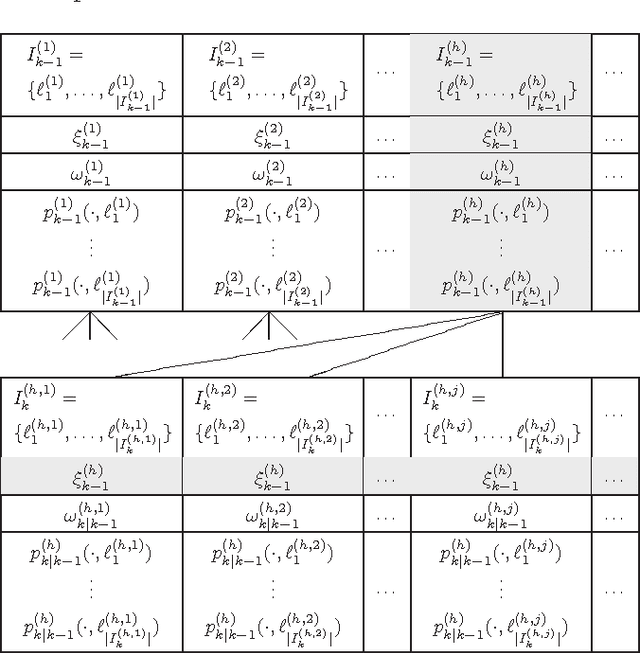
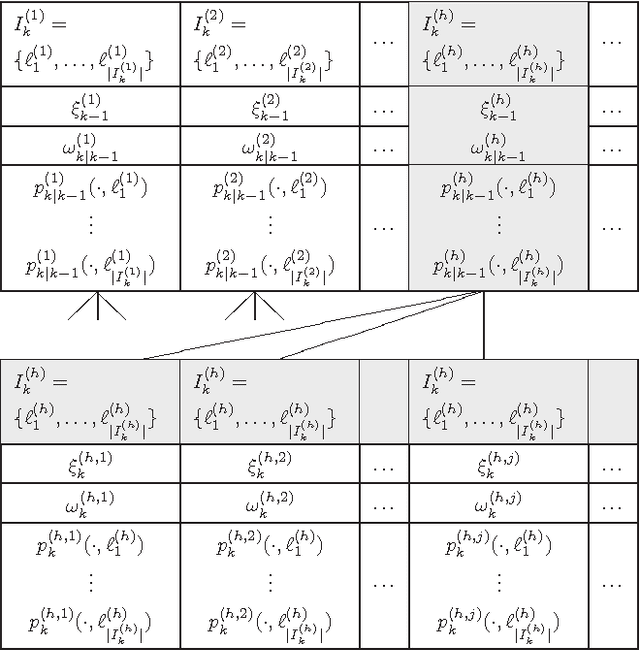
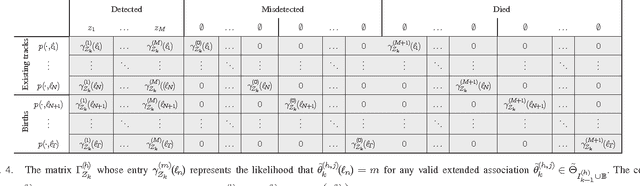
This paper proposes an efficient implementation of the generalized labeled multi-Bernoulli (GLMB) filter by combining the prediction and update into a single step. In contrast to the original approach which involves separate truncations in the prediction and update steps, the proposed implementation requires only one single truncation for each iteration, which can be performed using a standard ranked optimal assignment algorithm. Furthermore, we propose a new truncation technique based on Markov Chain Monte Carlo methods such as Gibbs sampling, which drastically reduces the complexity of the filter. The superior performance of the proposed approach is demonstrated through extensive numerical studies.