Model-Based Multiple Instance Learning

While Multiple Instance (MI) data are point patterns -- sets or multi-sets of unordered points -- appropriate statistical point pattern models have not been used in MI learning. This article proposes a framework for model-based MI learning using point process theory. Likelihood functions for point pattern data derived from point process theory enable principled yet conceptually transparent extensions of learning tasks, such as classification, novelty detection and clustering, to point pattern data. Furthermore, tractable point pattern models as well as solutions for learning and decision making from point pattern data are developed.

Multiple Instance Learning with the Optimal Sub-Pattern Assignment Metric

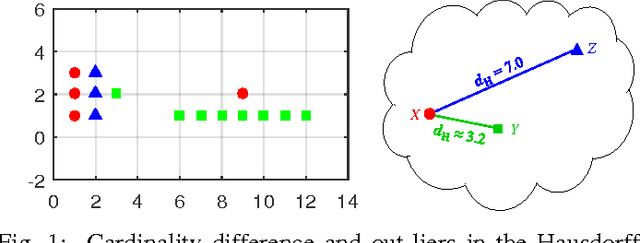
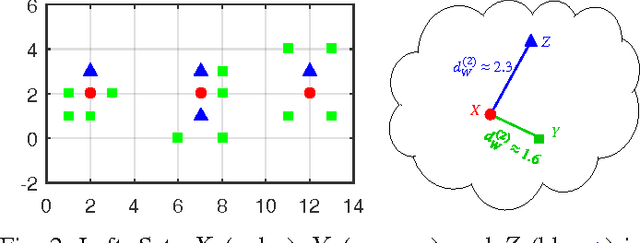
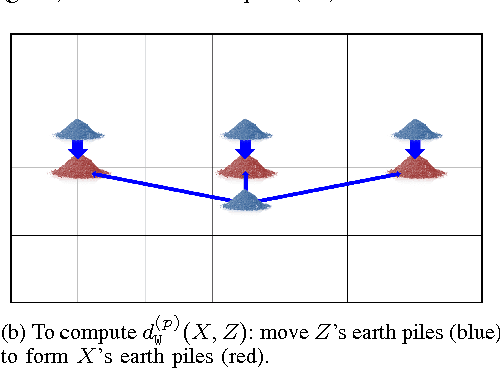
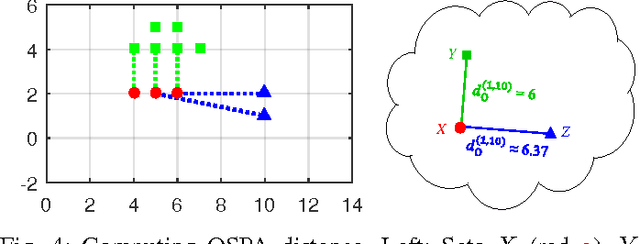
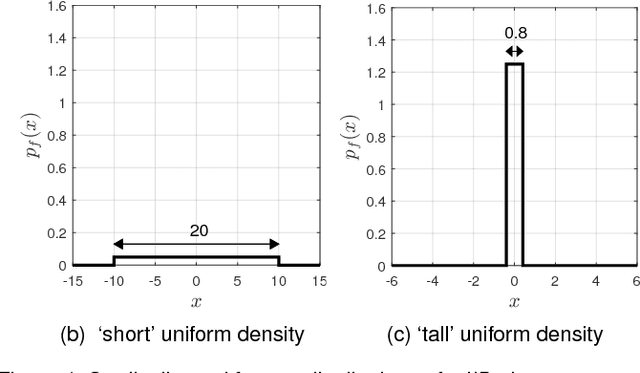
Multiple instance data are sets or multi-sets of unordered elements. Using metrics or distances for sets, we propose an approach to several multiple instance learning tasks, such as clustering (unsupervised learning), classification (supervised learning), and novelty detection (semi-supervised learning). In particular, we introduce the Optimal Sub-Pattern Assignment metric to multiple instance learning so as to provide versatile design choices. Numerical experiments on both simulated and real data are presented to illustrate the versatility of the proposed solution.

Model-based Classification and Novelty Detection For Point Pattern Data

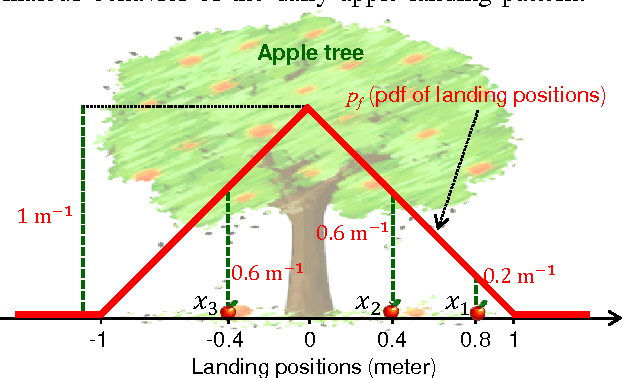
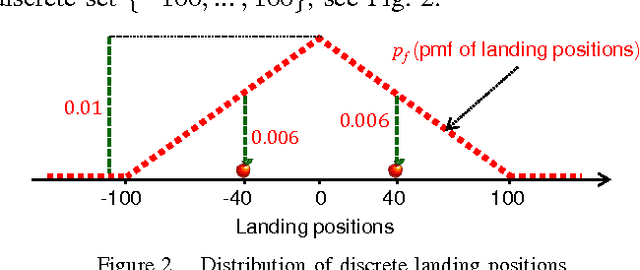
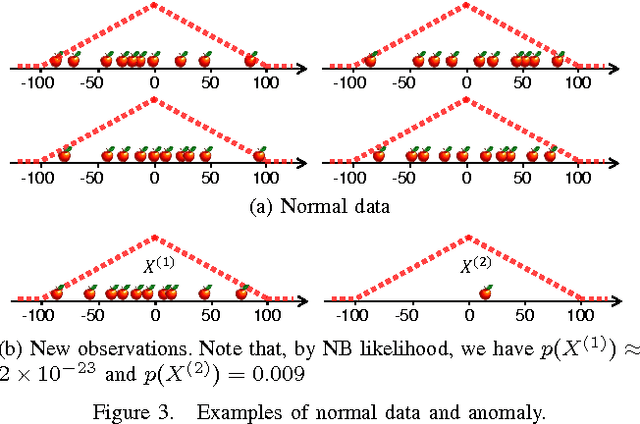
Point patterns are sets or multi-sets of unordered elements that can be found in numerous data sources. However, in data analysis tasks such as classification and novelty detection, appropriate statistical models for point pattern data have not received much attention. This paper proposes the modelling of point pattern data via random finite sets (RFS). In particular, we propose appropriate likelihood functions, and a maximum likelihood estimator for learning a tractable family of RFS models. In novelty detection, we propose novel ranking functions based on RFS models, which substantially improve performance.

Clustering For Point Pattern Data

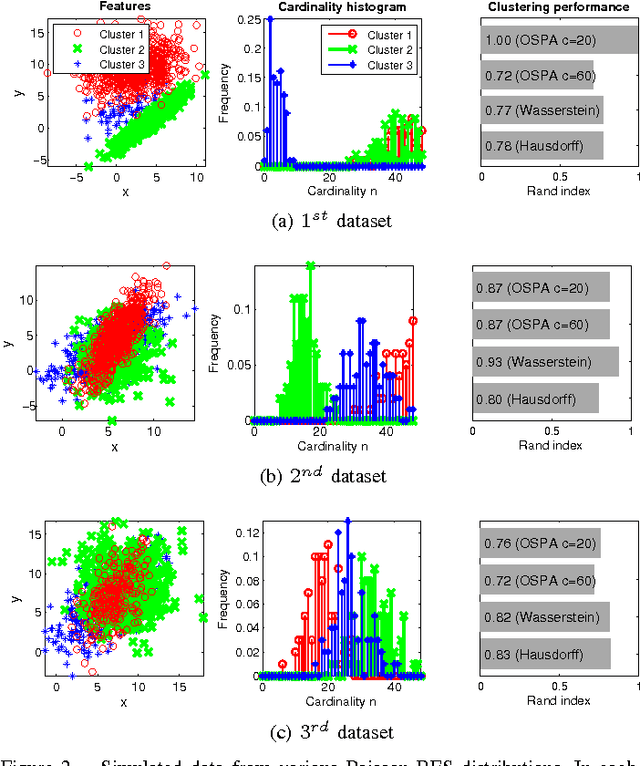
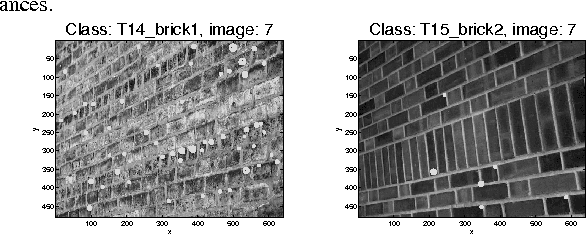
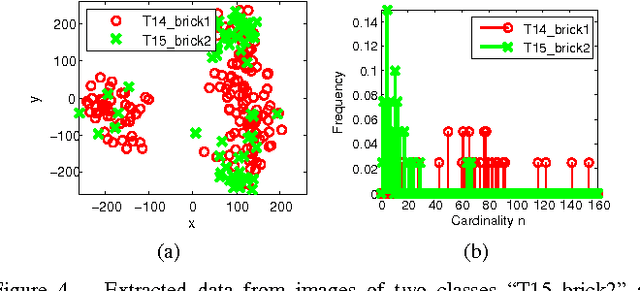
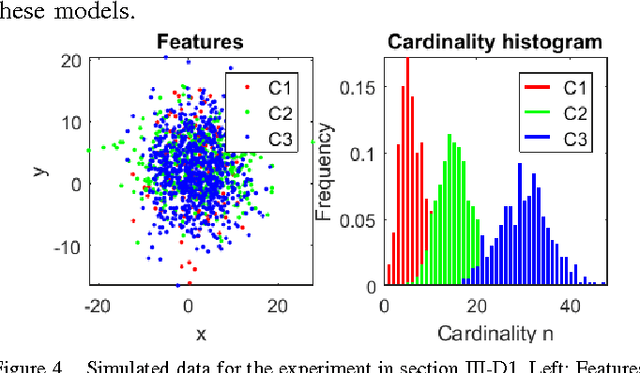
Clustering is one of the most common unsupervised learning tasks in machine learning and data mining. Clustering algorithms have been used in a plethora of applications across several scientific fields. However, there has been limited research in the clustering of point patterns - sets or multi-sets of unordered elements - that are found in numerous applications and data sources. In this paper, we propose two approaches for clustering point patterns. The first is a non-parametric method based on novel distances for sets. The second is a model-based approach, formulated via random finite set theory, and solved by the Expectation-Maximization algorithm. Numerical experiments show that the proposed methods perform well on both simulated and real data.