Linear Complexity Gibbs Sampling for Generalized Labeled Multi-Bernoulli Filtering

Generalized Labeled Multi-Bernoulli (GLMB) densities arise in a host of multi-object system applications analogous to Gaussians in single-object filtering. However, computing the GLMB filtering density requires solving NP-hard problems. To alleviate this computational bottleneck, we develop a linear complexity Gibbs sampling framework for GLMB density computation. Specifically, we propose a tempered Gibbs sampler that exploits the structure of the GLMB filtering density to achieve an $\mathcal{O}(T(P+M))$ complexity, where $T$ is the number of iterations of the algorithm, $P$ and $M$ are the number hypothesized objects and measurements. This innovation enables an $\mathcal{O}(T(P+M+\log(T))+PM)$ complexity implementation of the GLMB filter. Convergence of the proposed Gibbs sampler is established and numerical studies are presented to validate the proposed GLMB filter implementation.

A Bayesian 3D Multi-view Multi-object Tracking Filter

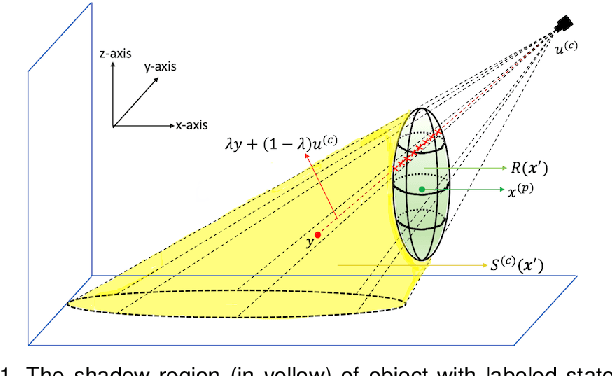
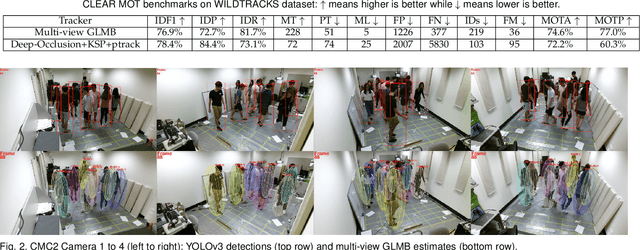
This paper proposes an online multi-camera multi-object tracker that only requires monocular detector training, independent of the multi-camera configurations, allowing seamless extension/deletion of cameras without (retraining) effort. The proposed algorithm has a linear complexity in the total number of detections across the cameras, and hence scales gracefully with the number of cameras. It operates in 3D world frame, and provides 3D trajectory estimates of the objects. The key innovation is a high fidelity yet tractable 3D occlusion model, amenable to optimal Bayesian multi-view multi-object filtering, which seamlessly integrates, into a single Bayesian recursion, the sub-tasks of track management, state estimation, clutter rejection, and occlusion/misdetection handling. The proposed algorithm is evaluated on the latest WILDTRACKS dataset, and demonstrated to work in very crowded scenes on a new dataset.