Cenek Albl
3D Reconstruction from public webcams
Aug 21, 2021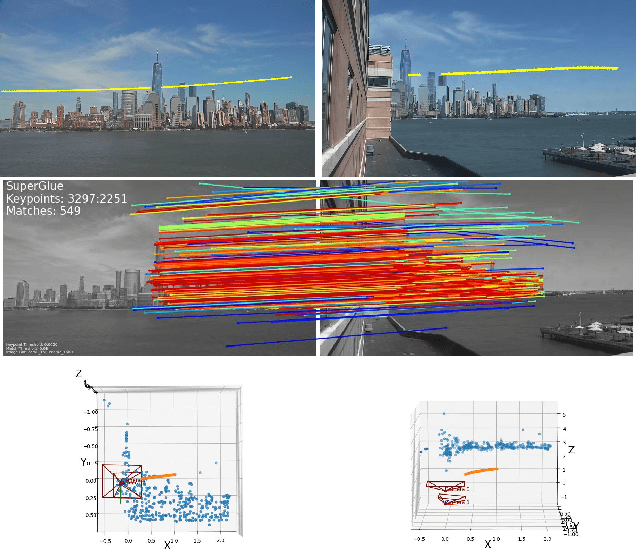
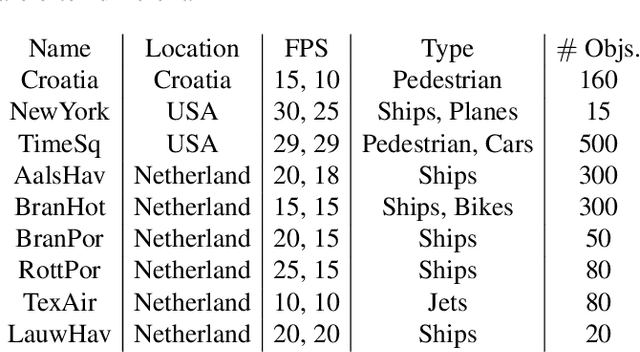
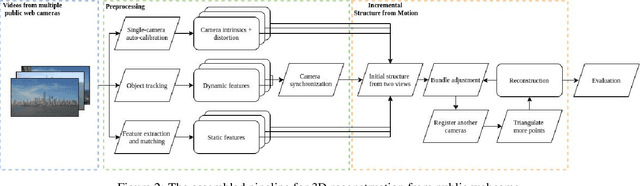
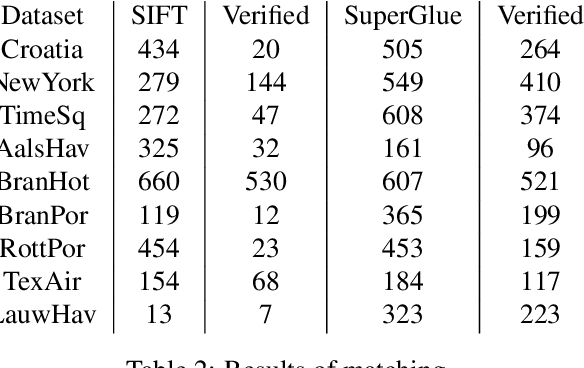
Abstract:In this paper, we investigate the possibility of reconstructing the 3D geometry of a scene captured by multiple webcams. The number of publicly accessible webcams is already large and it is growing every day. A logical question arises - can we use this free source of data for something beyond leisure activities? The challenge is that no internal, external, or temporal calibration of these cameras is available. We show that using recent advances in computer vision, we successfully calibrate the cameras, perform 3D reconstructions of the static scene and also recover the 3D trajectories of moving objects.
From two rolling shutters to one global shutter
Jun 02, 2020



Abstract:Most consumer cameras are equipped with electronic rolling shutter, leading to image distortions when the camera moves during image capture. We explore a surprisingly simple camera configuration that makes it possible to undo the rolling shutter distortion: two cameras mounted to have different rolling shutter directions. Such a setup is easy and cheap to build and it possesses the geometric constraints needed to correct rolling shutter distortion using only a sparse set of point correspondences between the two images. We derive equations that describe the underlying geometry for general and special motions and present an efficient method for finding their solutions. Our synthetic and real experiments demonstrate that our approach is able to remove large rolling shutter distortions of all types without relying on any specific scene structure.
Minimal Rolling Shutter Absolute Pose with Unknown Focal Length and Radial Distortion
Apr 29, 2020



Abstract:The internal geometry of most modern consumer cameras is not adequately described by the perspective projection. Almost all cameras exhibit some radial lens distortion and are equipped with an electronic rolling shutter that induces distortions when the camera moves during the image capture. When focal length has not been calibrated offline, the parameters that describe the radial and rolling shutter distortions are usually unknown. While for global shutter cameras, minimal solvers for the absolute camera pose and unknown focal length and radial distortion are available, solvers for the rolling shutter were missing. We present the first minimal solutions for the absolute pose of a rolling shutter camera with unknown rolling shutter parameters, focal length, and radial distortion. Our new minimal solvers combine iterative schemes designed for calibrated rolling shutter cameras with fast generalized eigenvalue and Groebner basis solvers. In a series of experiments, with both synthetic and real data, we show that our new solvers provide accurate estimates of the camera pose, rolling shutter parameters, focal length, and radial distortion parameters.
Reconstruction of 3D flight trajectories from ad-hoc camera networks
Mar 10, 2020



Abstract:We present a method to reconstruct the 3D trajectory of an airborne robotic system only from videos recorded with cameras that are unsynchronized, may feature rolling shutter distortion, and whose viewpoints are unknown. Our approach enables robust and accurate outside-in tracking of dynamically flying targets, with cheap and easy-to-deploy equipment. We show that, in spite of the weakly constrained setting, recent developments in computer vision make it possible to reconstruct trajectories in 3D from unsynchronized, uncalibrated networks of consumer cameras, and validate the proposed method in a realistic field experiment. We make our code available along with the data, including cm-accurate ground-truth from differential GNSS navigation.
Linear solution to the minimal absolute pose rolling shutter problem
Dec 30, 2018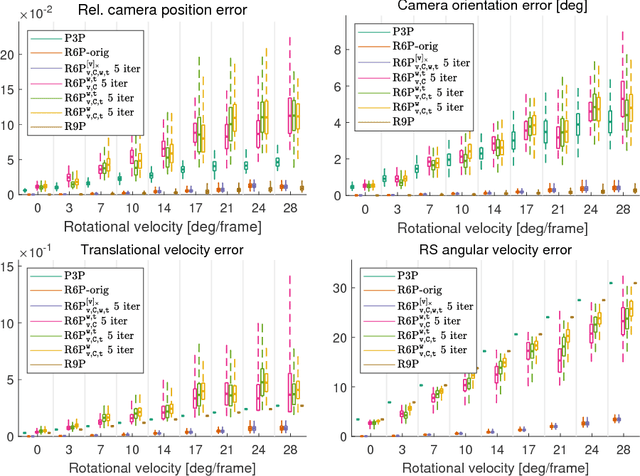

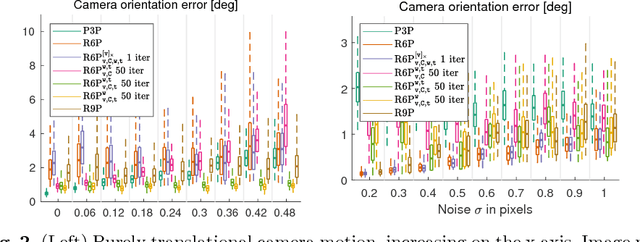
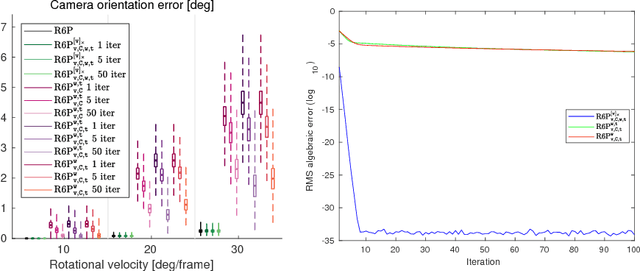
Abstract:This paper presents new efficient solutions to the rolling shutter camera absolute pose problem. Unlike the state-of-the-art polynomial solvers, we approach the problem using simple and fast linear solvers in an iterative scheme. We present several solutions based on fixing different sets of variables and investigate the performance of them thoroughly. We design a new alternation strategy that estimates all parameters in each iteration linearly by fixing just the non-linear terms. Our best 6-point solver, based on the new alternation technique, shows an identical or even better performance than the state-of-the-art R6P solver and is two orders of magnitude faster. In addition, a linear non-iterative solver is presented that requires a non-minimal number of 9 correspondences but provides even better results than the state-of-the-art R6P. Moreover, all proposed linear solvers provide a single solution while the state-of-the-art R6P provides up to 20 solutions which have to be pruned by expensive verification.
On the Two-View Geometry of Unsynchronized Cameras
Apr 22, 2017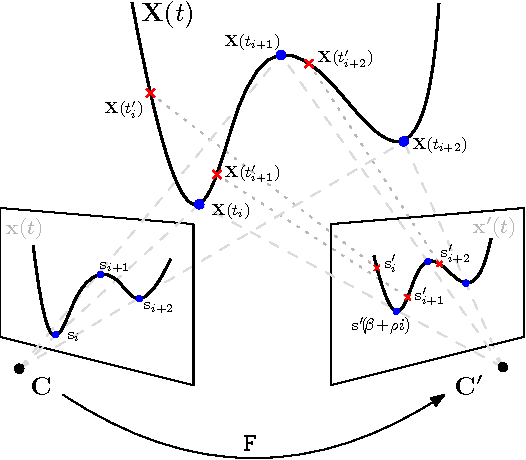

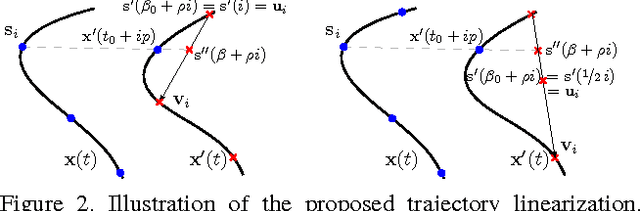
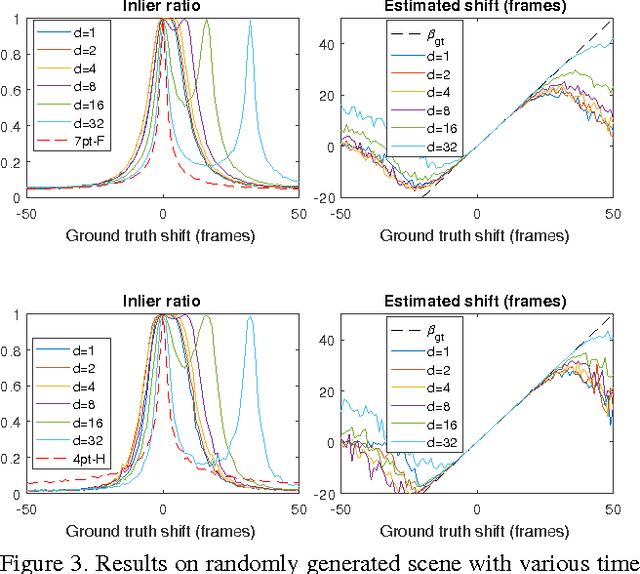
Abstract:We present new methods for simultaneously estimating camera geometry and time shift from video sequences from multiple unsynchronized cameras. Algorithms for simultaneous computation of a fundamental matrix or a homography with unknown time shift between images are developed. Our methods use minimal correspondence sets (eight for fundamental matrix and four and a half for homography) and therefore are suitable for robust estimation using RANSAC. Furthermore, we present an iterative algorithm that extends the applicability on sequences which are significantly unsynchronized, finding the correct time shift up to several seconds. We evaluated the methods on synthetic and wide range of real world datasets and the results show a broad applicability to the problem of camera synchronization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge