Jan Heller
LAAS, CTU/FEE
On the Two-View Geometry of Unsynchronized Cameras
Apr 22, 2017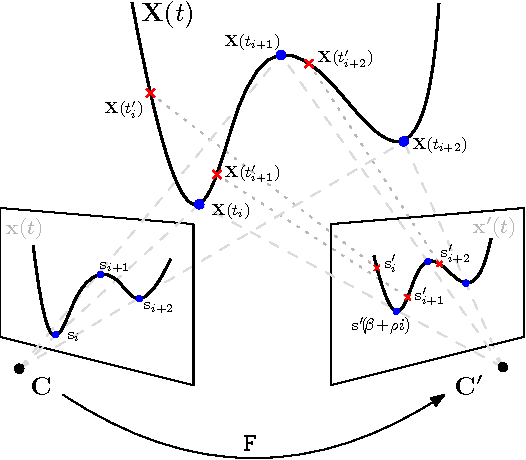

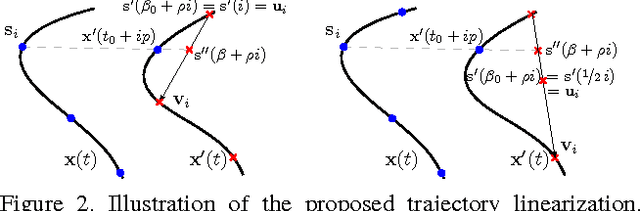
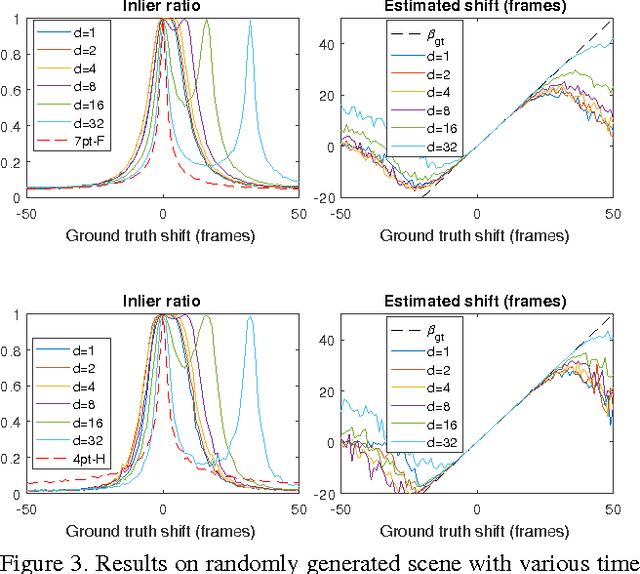
Abstract:We present new methods for simultaneously estimating camera geometry and time shift from video sequences from multiple unsynchronized cameras. Algorithms for simultaneous computation of a fundamental matrix or a homography with unknown time shift between images are developed. Our methods use minimal correspondence sets (eight for fundamental matrix and four and a half for homography) and therefore are suitable for robust estimation using RANSAC. Furthermore, we present an iterative algorithm that extends the applicability on sequences which are significantly unsynchronized, finding the correct time shift up to several seconds. We evaluated the methods on synthetic and wide range of real world datasets and the results show a broad applicability to the problem of camera synchronization.
Hand-Eye and Robot-World Calibration by Global Polynomial Optimization
Feb 13, 2014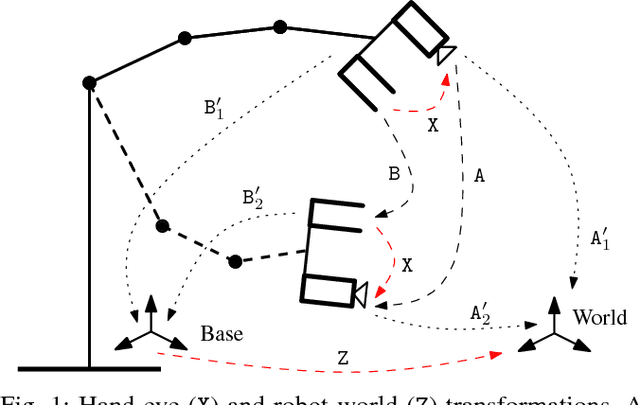
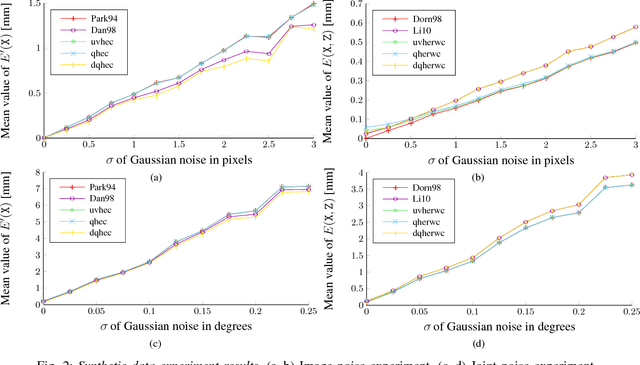

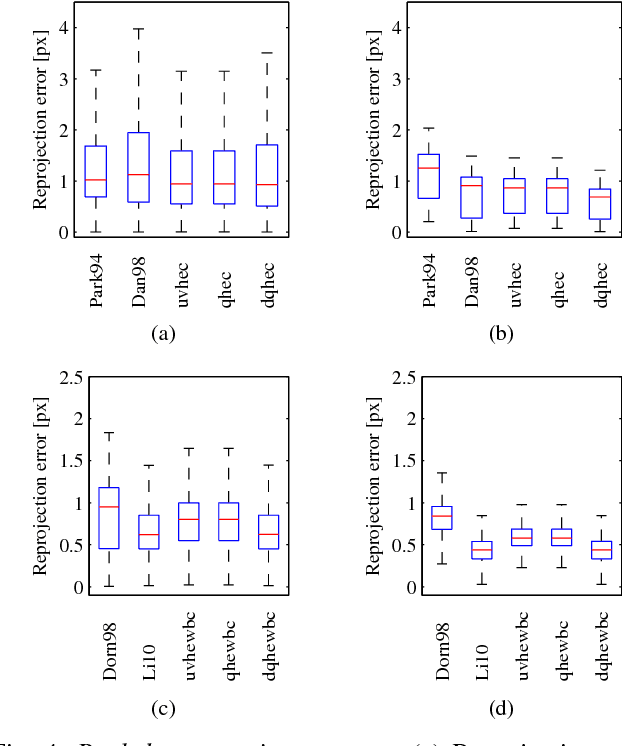
Abstract:The need to relate measurements made by a camera to a different known coordinate system arises in many engineering applications. Historically, it appeared for the first time in the connection with cameras mounted on robotic systems. This problem is commonly known as hand-eye calibration. In this paper, we present several formulations of hand-eye calibration that lead to multivariate polynomial optimization problems. We show that the method of convex linear matrix inequality (LMI) relaxations can be used to effectively solve these problems and to obtain globally optimal solutions. Further, we show that the same approach can be used for the simultaneous hand-eye and robot-world calibration. Finally, we validate the proposed solutions using both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge