Hand-Eye and Robot-World Calibration by Global Polynomial Optimization
Paper and Code
Feb 13, 2014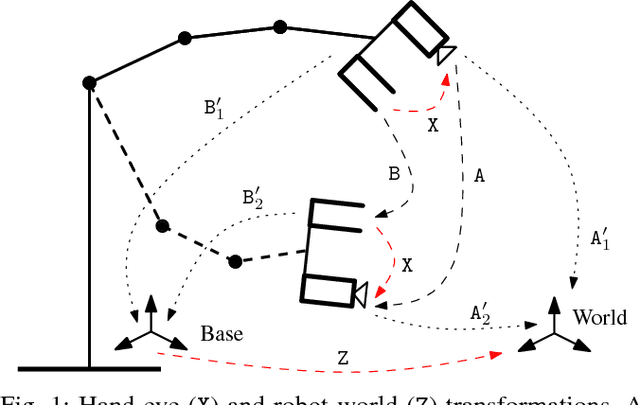
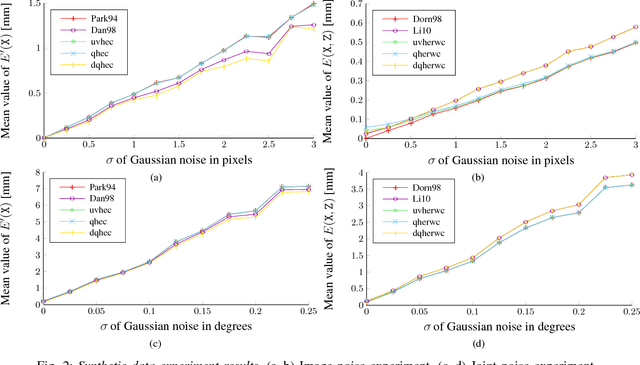

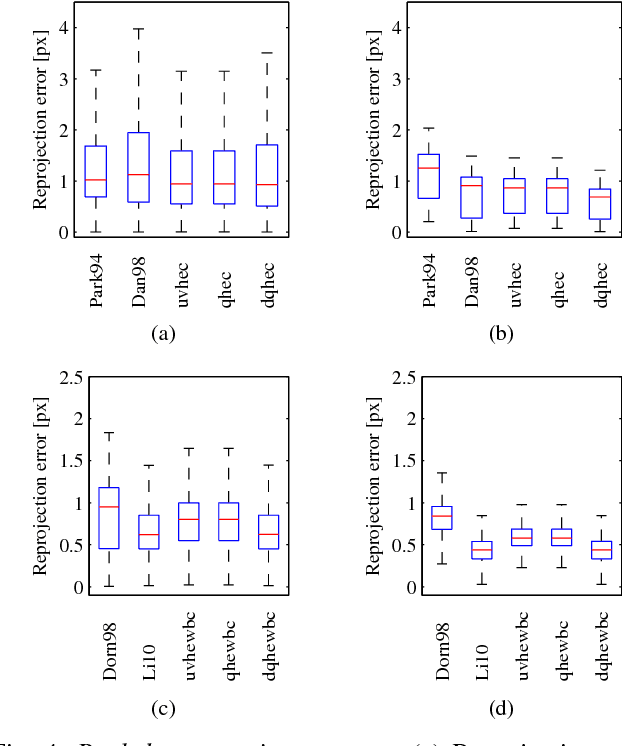
The need to relate measurements made by a camera to a different known coordinate system arises in many engineering applications. Historically, it appeared for the first time in the connection with cameras mounted on robotic systems. This problem is commonly known as hand-eye calibration. In this paper, we present several formulations of hand-eye calibration that lead to multivariate polynomial optimization problems. We show that the method of convex linear matrix inequality (LMI) relaxations can be used to effectively solve these problems and to obtain globally optimal solutions. Further, we show that the same approach can be used for the simultaneous hand-eye and robot-world calibration. Finally, we validate the proposed solutions using both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge