Globally Optimal Solution to Inverse Kinematics of 7DOF Serial Manipulator

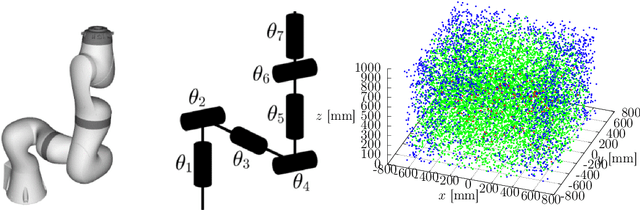
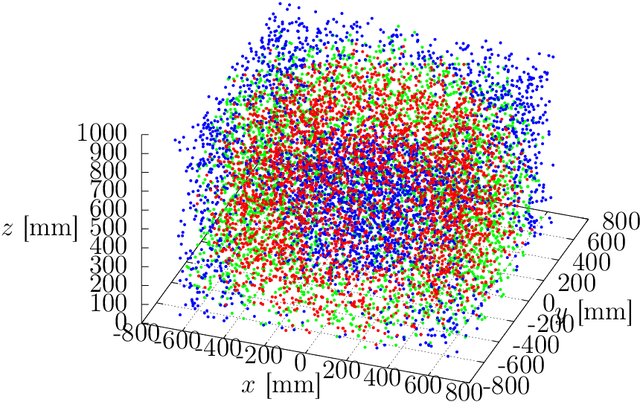
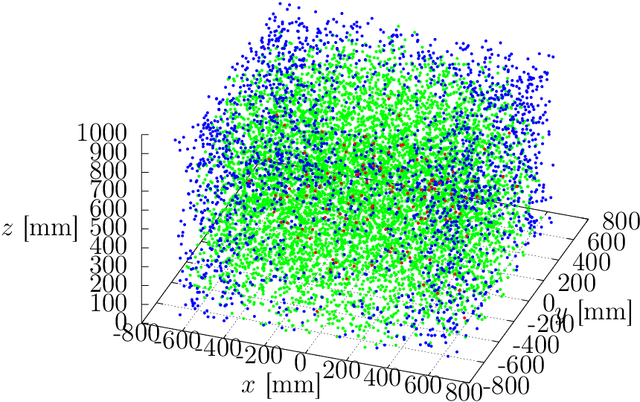
The Inverse Kinematics (IK) problem is to nd robot control parameters to bring it into the desired position under the kinematics and collision constraints. We present a global solution to the optimal IK problem for a general serial 7DOF manipulator with revolute joints and a quadratic polynomial objective function. We show that the kinematic constraints due to rotations can all be generated by second-degree polynomials. This is important since it signicantly simplies further step where we nd the optimal solution by Lasserre relaxations of non-convex polynomial systems. We demonstrate that the second relaxation is sucient to solve the 7DOF IK problem. Our approach is certiably globally optimal. We demonstrate the method on the 7DOF KUKA LBR IIWA manipulator and show that we are able to compute the optimal IK or certify in-feasibility in 99 % tested poses.

Approximating Pareto Curves using Semidefinite Relaxations

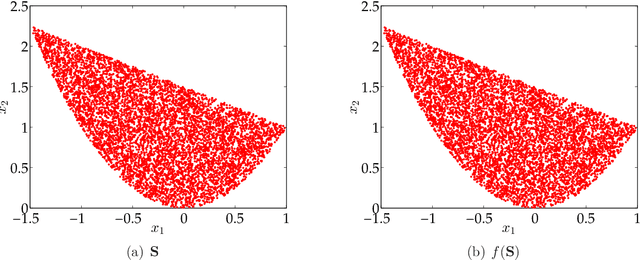
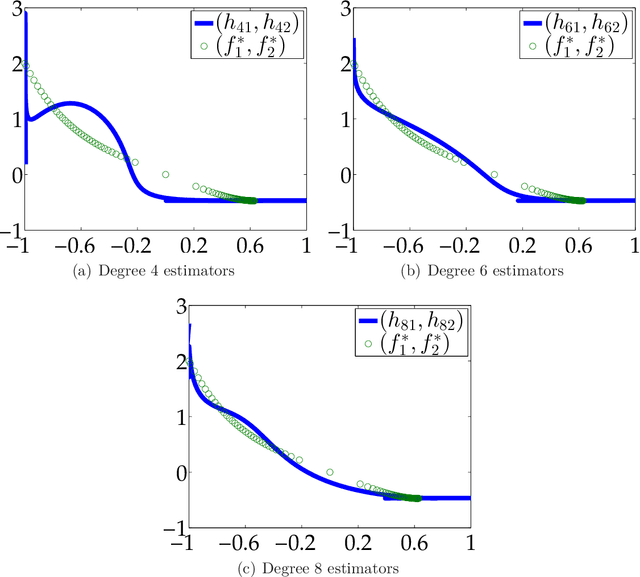
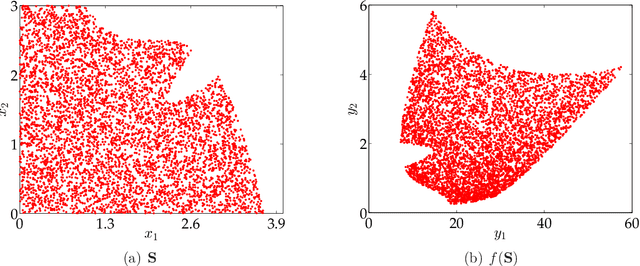
We consider the problem of constructing an approximation of the Pareto curve associated with the multiobjective optimization problem $\min_{\mathbf{x} \in \mathbf{S}}\{ (f_1(\mathbf{x}), f_2(\mathbf{x})) \}$, where $f_1$ and $f_2$ are two conflicting polynomial criteria and $\mathbf{S} \subset \mathbb{R}^n$ is a compact basic semialgebraic set. We provide a systematic numerical scheme to approximate the Pareto curve. We start by reducing the initial problem into a scalarized polynomial optimization problem (POP). Three scalarization methods lead to consider different parametric POPs, namely (a) a weighted convex sum approximation, (b) a weighted Chebyshev approximation, and (c) a parametric sublevel set approximation. For each case, we have to solve a semidefinite programming (SDP) hierarchy parametrized by the number of moments or equivalently the degree of a polynomial sums of squares approximation of the Pareto curve. When the degree of the polynomial approximation tends to infinity, we provide guarantees of convergence to the Pareto curve in $L^2$-norm for methods (a) and (b), and $L^1$-norm for method (c).

Hand-Eye and Robot-World Calibration by Global Polynomial Optimization

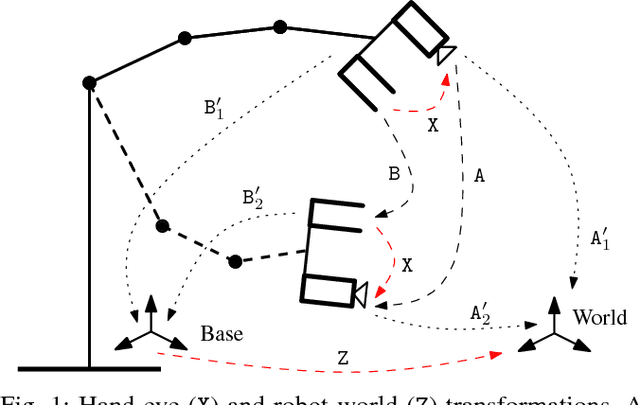
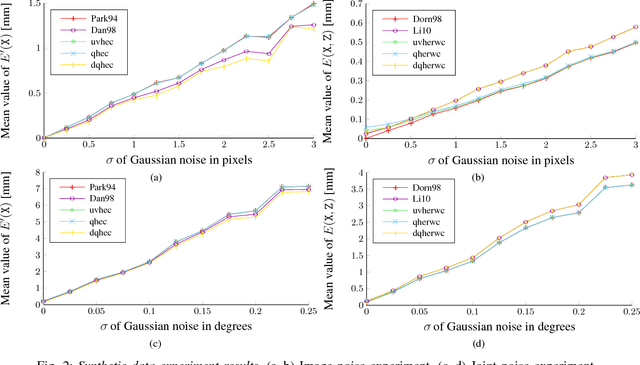
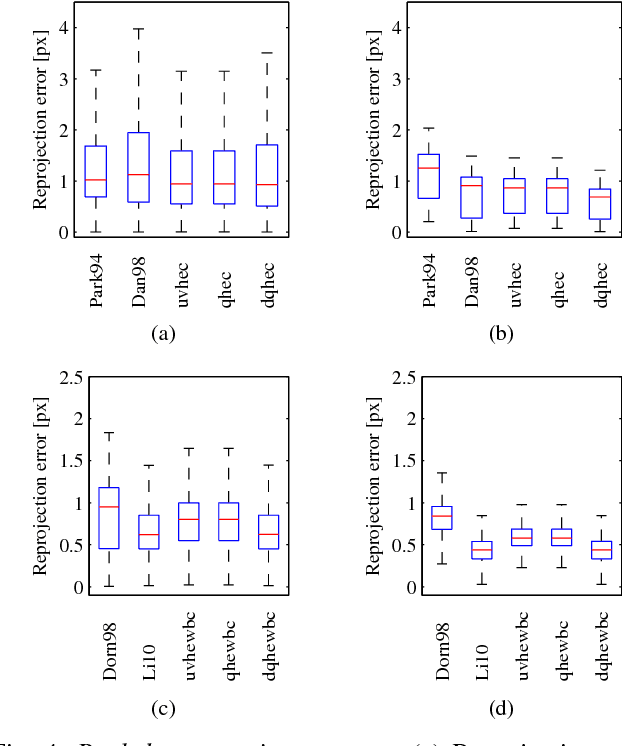
The need to relate measurements made by a camera to a different known coordinate system arises in many engineering applications. Historically, it appeared for the first time in the connection with cameras mounted on robotic systems. This problem is commonly known as hand-eye calibration. In this paper, we present several formulations of hand-eye calibration that lead to multivariate polynomial optimization problems. We show that the method of convex linear matrix inequality (LMI) relaxations can be used to effectively solve these problems and to obtain globally optimal solutions. Further, we show that the same approach can be used for the simultaneous hand-eye and robot-world calibration. Finally, we validate the proposed solutions using both synthetic and real datasets.