Verifying Properties of Binary Neural Networks Using Sparse Polynomial Optimization

This paper explores methods for verifying the properties of Binary Neural Networks (BNNs), focusing on robustness against adversarial attacks. Despite their lower computational and memory needs, BNNs, like their full-precision counterparts, are also sensitive to input perturbations. Established methods for solving this problem are predominantly based on Satisfiability Modulo Theories and Mixed-Integer Linear Programming techniques, which are characterized by NP complexity and often face scalability issues. We introduce an alternative approach using Semidefinite Programming relaxations derived from sparse Polynomial Optimization. Our approach, compatible with continuous input space, not only mitigates numerical issues associated with floating-point calculations but also enhances verification scalability through the strategic use of tighter first-order semidefinite relaxations. We demonstrate the effectiveness of our method in verifying robustness against both $\|.\|_\infty$ and $\|.\|_2$-based adversarial attacks.

Local Lipschitz Constant Computation of ReLU-FNNs: Upper Bound Computation with Exactness Verification

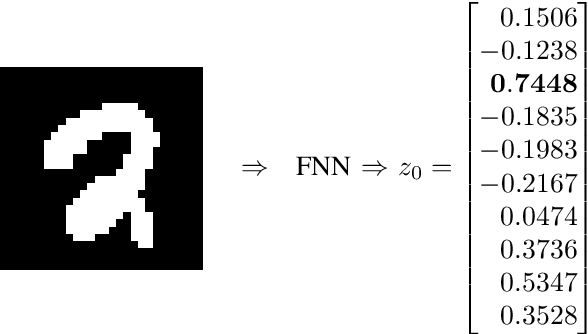
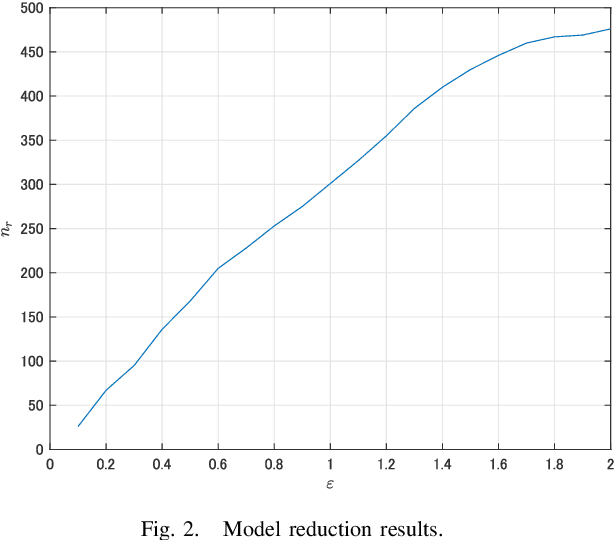
This paper is concerned with the computation of the local Lipschitz constant of feedforward neural networks (FNNs) with activation functions being rectified linear units (ReLUs). The local Lipschitz constant of an FNN for a target input is a reasonable measure for its quantitative evaluation of the reliability. By following a standard procedure using multipliers that capture the behavior of ReLUs,we first reduce the upper bound computation problem of the local Lipschitz constant into a semidefinite programming problem (SDP). Here we newly introduce copositive multipliers to capture the ReLU behavior accurately. Then, by considering the dual of the SDP for the upper bound computation, we second derive a viable test to conclude the exactness of the computed upper bound. However, these SDPs are intractable for practical FNNs with hundreds of ReLUs. To address this issue, we further propose a method to construct a reduced order model whose input-output property is identical to the original FNN over a neighborhood of the target input. We finally illustrate the effectiveness of the model reduction and exactness verification methods with numerical examples of practical FNNs.

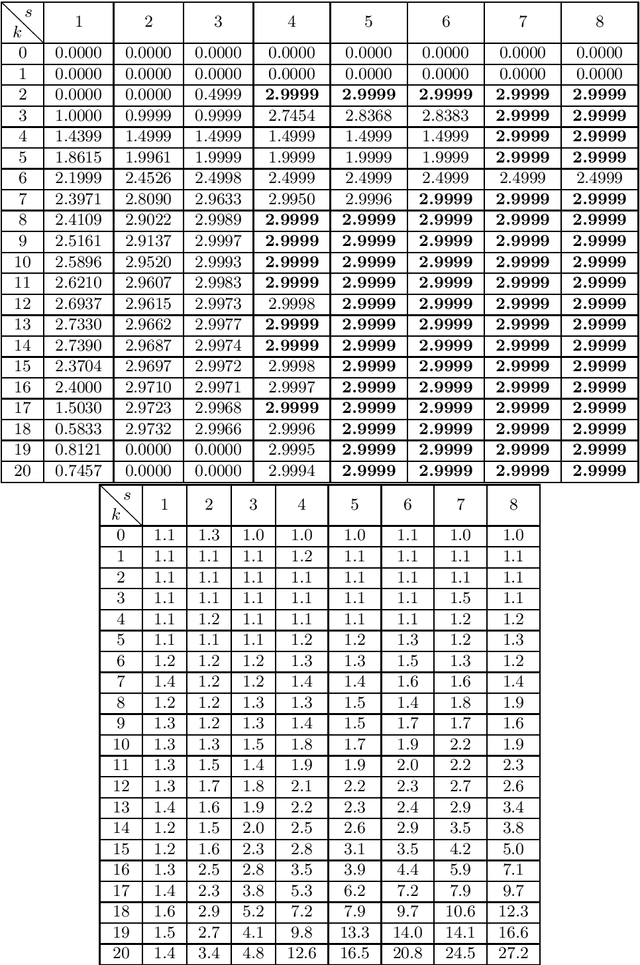
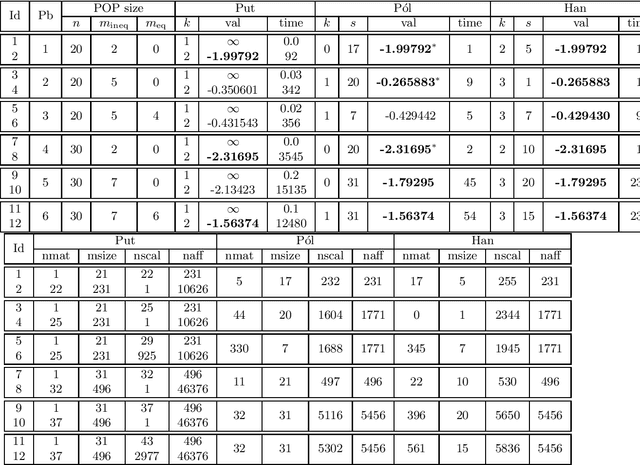
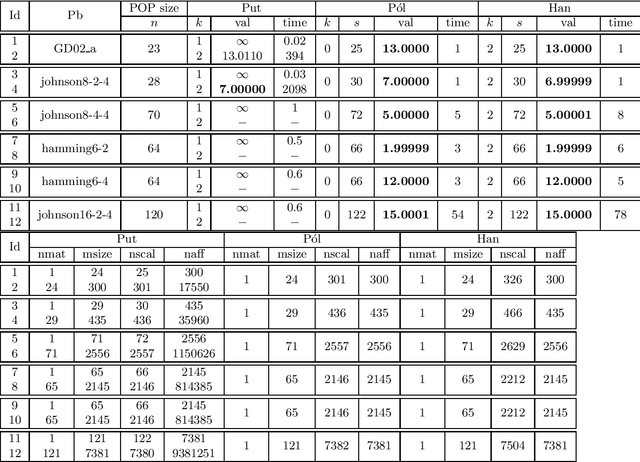
Tractable hierarchies of convex relaxations for polynomial optimization on the nonnegative orthant

We consider polynomial optimization problems (POP) on a semialgebraic set contained in the nonnegative orthant (every POP on a compact set can be put in this format by a simple translation of the origin). Such a POP can be converted to an equivalent POP by squaring each variable. Using even symmetry and the concept of factor width, we propose a hierarchy of semidefinite relaxations based on the extension of P\'olya's Positivstellensatz by Dickinson-Povh. As its distinguishing and crucial feature, the maximal matrix size of each resulting semidefinite relaxation can be chosen arbitrarily and in addition, we prove that the sequence of values returned by the new hierarchy converges to the optimal value of the original POP at the rate $O(\varepsilon^{-c})$ if the semialgebraic set has nonempty interior. When applied to (i) robustness certification of multi-layer neural networks and (ii) computation of positive maximal singular values, our method based on P\'olya's Positivstellensatz provides better bounds and runs several hundred times faster than the standard Moment-SOS hierarchy.

Sparse Polynomial Optimization: Theory and Practice

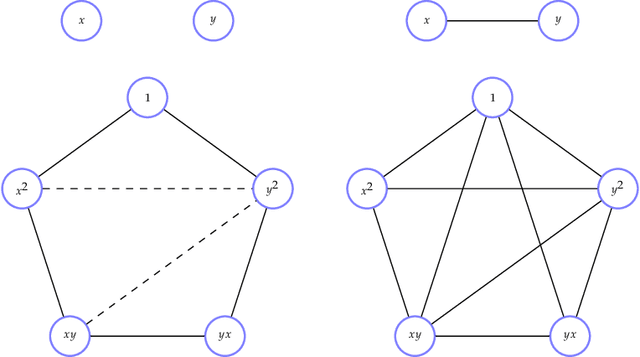
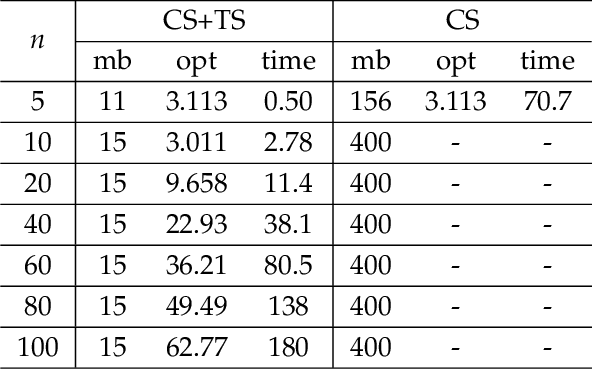
The problem of minimizing a polynomial over a set of polynomial inequalities is an NP-hard non-convex problem. Thanks to powerful results from real algebraic geometry, one can convert this problem into a nested sequence of finite-dimensional convex problems. At each step of the associated hierarchy, one needs to solve a fixed size semidefinite program, which can be in turn solved with efficient numerical tools. On the practical side however, there is no-free lunch and such optimization methods usually encompass severe scalability issues. Fortunately, for many applications, we can look at the problem in the eyes and exploit the inherent data structure arising from the cost and constraints describing the problem, for instance sparsity or symmetries. This book presents several research efforts to tackle this scientific challenge with important computational implications, and provides the development of alternative optimization schemes that scale well in terms of computational complexity, at least in some identified class of problems. The presented algorithmic framework in this book mainly exploits the sparsity structure of the input data to solve large-scale polynomial optimization problems. We present sparsity-exploiting hierarchies of relaxations, for either unconstrained or constrained problems. By contrast with the dense hierarchies, they provide faster approximation of the solution in practice but also come with the same theoretical convergence guarantees. Our framework is not restricted to static polynomial optimization, and we expose hierarchies of approximations for values of interest arising from the analysis of dynamical systems. We also present various extensions to problems involving noncommuting variables, e.g., matrices of arbitrary size or quantum physic operators.

Stability Analysis of Recurrent Neural Networks by IQC with Copositive Mutipliers

This paper is concerned with the stability analysis of the recurrent neural networks (RNNs) by means of the integral quadratic constraint (IQC) framework. The rectified linear unit (ReLU) is typically employed as the activation function of the RNN, and the ReLU has specific nonnegativity properties regarding its input and output signals. Therefore, it is effective if we can derive IQC-based stability conditions with multipliers taking care of such nonnegativity properties. However, such nonnegativity (linear) properties are hardly captured by the existing multipliers defined on the positive semidefinite cone. To get around this difficulty, we loosen the standard positive semidefinite cone to the copositive cone, and employ copositive multipliers to capture the nonnegativity properties. We show that, within the framework of the IQC, we can employ copositive multipliers (or their inner approximation) together with existing multipliers such as Zames-Falb multipliers and polytopic bounding multipliers, and this directly enables us to ensure that the introduction of the copositive multipliers leads to better (no more conservative) results. We finally illustrate the effectiveness of the IQC-based stability conditions with the copositive multipliers by numerical examples.

Polynomial Optimization for Bounding Lipschitz Constants of Deep Networks

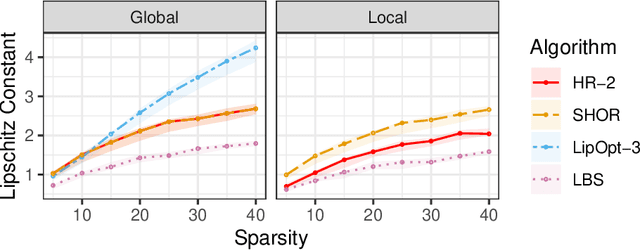
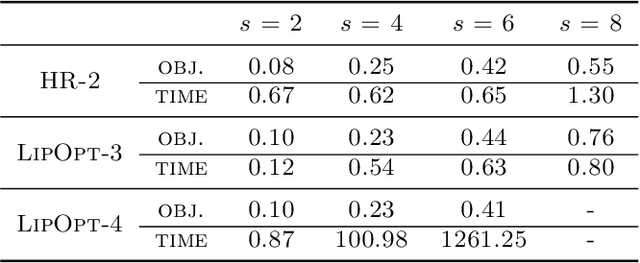
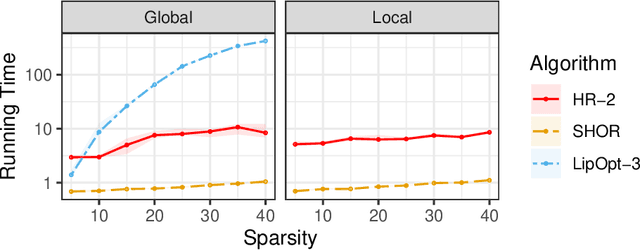
The Lipschitz constant of a network plays an important role in many applications of deep learning, such as robustness certification and Wasserstein Generative Adversarial Network. We introduce a semidefinite programming hierarchy to estimate the global and local Lipschitz constant of a multiple layer deep neural network. The novelty is to combine a polynomial lifting for ReLU functions derivatives with a weak generalization of Putinar's positivity certificate. This idea could also apply to other, nearly sparse, polynomial optimization problems in machine learning. We empirically demonstrate that our method not only runs faster than state-of-the-art linear programming based method, but also provides sharper bounds.

Approximating Pareto Curves using Semidefinite Relaxations

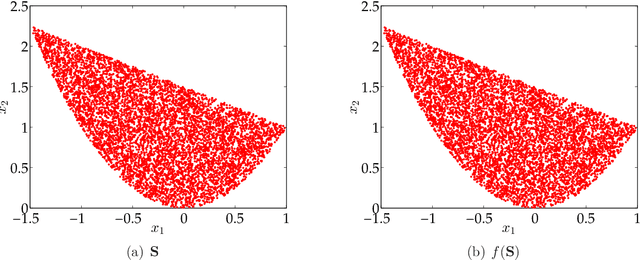
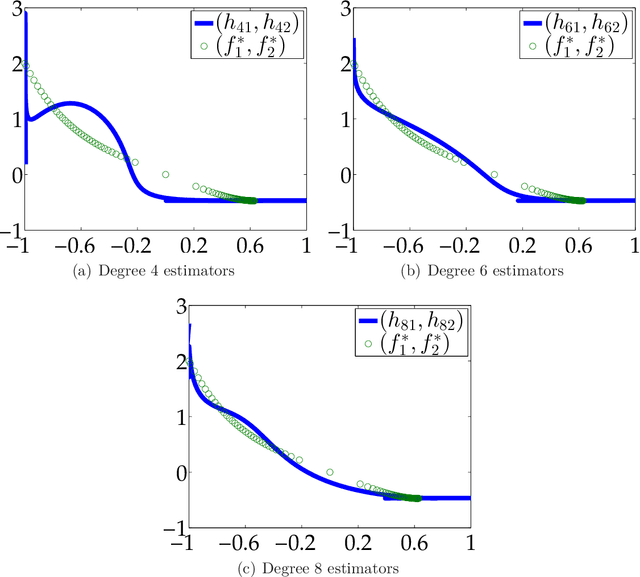
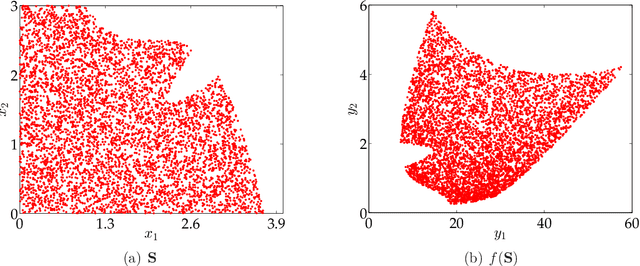
We consider the problem of constructing an approximation of the Pareto curve associated with the multiobjective optimization problem $\min_{\mathbf{x} \in \mathbf{S}}\{ (f_1(\mathbf{x}), f_2(\mathbf{x})) \}$, where $f_1$ and $f_2$ are two conflicting polynomial criteria and $\mathbf{S} \subset \mathbb{R}^n$ is a compact basic semialgebraic set. We provide a systematic numerical scheme to approximate the Pareto curve. We start by reducing the initial problem into a scalarized polynomial optimization problem (POP). Three scalarization methods lead to consider different parametric POPs, namely (a) a weighted convex sum approximation, (b) a weighted Chebyshev approximation, and (c) a parametric sublevel set approximation. For each case, we have to solve a semidefinite programming (SDP) hierarchy parametrized by the number of moments or equivalently the degree of a polynomial sums of squares approximation of the Pareto curve. When the degree of the polynomial approximation tends to infinity, we provide guarantees of convergence to the Pareto curve in $L^2$-norm for methods (a) and (b), and $L^1$-norm for method (c).