Yoshio Ebihara
Local Lipschitz Constant Computation of ReLU-FNNs: Upper Bound Computation with Exactness Verification
Oct 17, 2023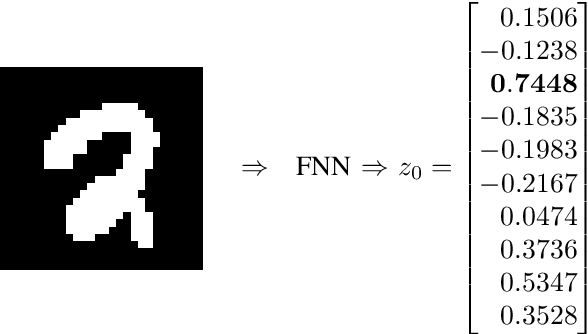
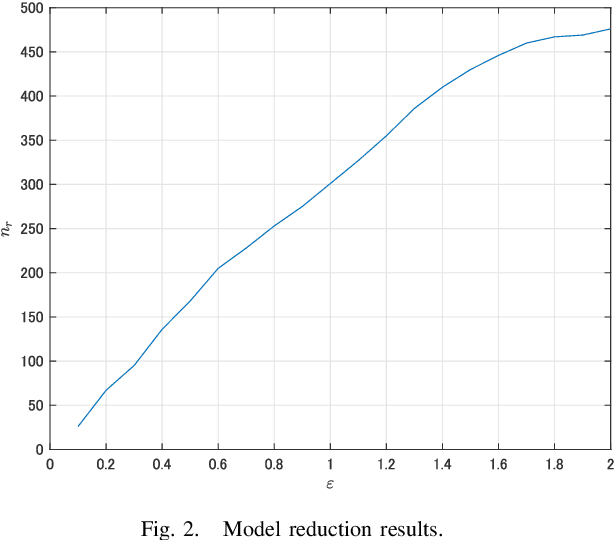

Abstract:This paper is concerned with the computation of the local Lipschitz constant of feedforward neural networks (FNNs) with activation functions being rectified linear units (ReLUs). The local Lipschitz constant of an FNN for a target input is a reasonable measure for its quantitative evaluation of the reliability. By following a standard procedure using multipliers that capture the behavior of ReLUs,we first reduce the upper bound computation problem of the local Lipschitz constant into a semidefinite programming problem (SDP). Here we newly introduce copositive multipliers to capture the ReLU behavior accurately. Then, by considering the dual of the SDP for the upper bound computation, we second derive a viable test to conclude the exactness of the computed upper bound. However, these SDPs are intractable for practical FNNs with hundreds of ReLUs. To address this issue, we further propose a method to construct a reduced order model whose input-output property is identical to the original FNN over a neighborhood of the target input. We finally illustrate the effectiveness of the model reduction and exactness verification methods with numerical examples of practical FNNs.
Stability Analysis of Recurrent Neural Networks by IQC with Copositive Mutipliers
Feb 09, 2022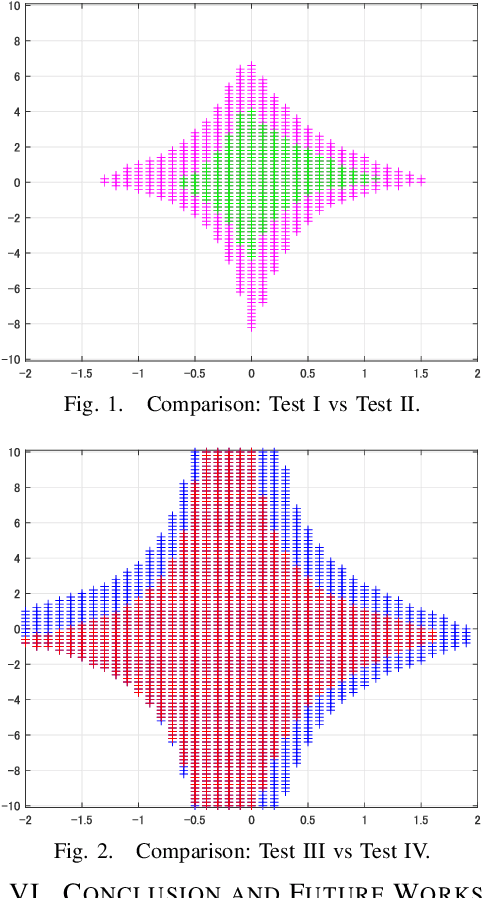
Abstract:This paper is concerned with the stability analysis of the recurrent neural networks (RNNs) by means of the integral quadratic constraint (IQC) framework. The rectified linear unit (ReLU) is typically employed as the activation function of the RNN, and the ReLU has specific nonnegativity properties regarding its input and output signals. Therefore, it is effective if we can derive IQC-based stability conditions with multipliers taking care of such nonnegativity properties. However, such nonnegativity (linear) properties are hardly captured by the existing multipliers defined on the positive semidefinite cone. To get around this difficulty, we loosen the standard positive semidefinite cone to the copositive cone, and employ copositive multipliers to capture the nonnegativity properties. We show that, within the framework of the IQC, we can employ copositive multipliers (or their inner approximation) together with existing multipliers such as Zames-Falb multipliers and polytopic bounding multipliers, and this directly enables us to ensure that the introduction of the copositive multipliers leads to better (no more conservative) results. We finally illustrate the effectiveness of the IQC-based stability conditions with the copositive multipliers by numerical examples.
* 6 pages, 2 figures. arXiv admin note: text overlap with arXiv:2011.12726
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge