Local Lipschitz Constant Computation of ReLU-FNNs: Upper Bound Computation with Exactness Verification

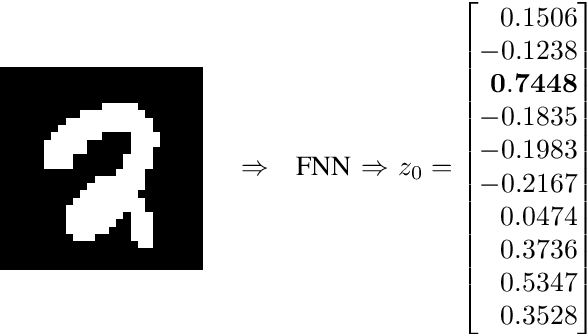
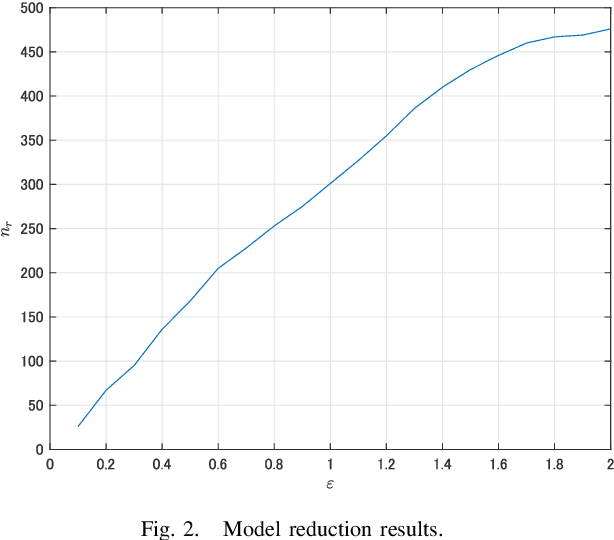
This paper is concerned with the computation of the local Lipschitz constant of feedforward neural networks (FNNs) with activation functions being rectified linear units (ReLUs). The local Lipschitz constant of an FNN for a target input is a reasonable measure for its quantitative evaluation of the reliability. By following a standard procedure using multipliers that capture the behavior of ReLUs,we first reduce the upper bound computation problem of the local Lipschitz constant into a semidefinite programming problem (SDP). Here we newly introduce copositive multipliers to capture the ReLU behavior accurately. Then, by considering the dual of the SDP for the upper bound computation, we second derive a viable test to conclude the exactness of the computed upper bound. However, these SDPs are intractable for practical FNNs with hundreds of ReLUs. To address this issue, we further propose a method to construct a reduced order model whose input-output property is identical to the original FNN over a neighborhood of the target input. We finally illustrate the effectiveness of the model reduction and exactness verification methods with numerical examples of practical FNNs.