Verifying Properties of Binary Neural Networks Using Sparse Polynomial Optimization

This paper explores methods for verifying the properties of Binary Neural Networks (BNNs), focusing on robustness against adversarial attacks. Despite their lower computational and memory needs, BNNs, like their full-precision counterparts, are also sensitive to input perturbations. Established methods for solving this problem are predominantly based on Satisfiability Modulo Theories and Mixed-Integer Linear Programming techniques, which are characterized by NP complexity and often face scalability issues. We introduce an alternative approach using Semidefinite Programming relaxations derived from sparse Polynomial Optimization. Our approach, compatible with continuous input space, not only mitigates numerical issues associated with floating-point calculations but also enhances verification scalability through the strategic use of tighter first-order semidefinite relaxations. We demonstrate the effectiveness of our method in verifying robustness against both $\|.\|_\infty$ and $\|.\|_2$-based adversarial attacks.

Uncertainty Quantification of Set-Membership Estimation in Control and Perception: Revisiting the Minimum Enclosing Ellipsoid

Set-membership estimation (SME) outputs a set estimator that guarantees to cover the groundtruth. Such sets are, however, defined by (many) abstract (and potentially nonconvex) constraints and therefore difficult to manipulate. We present tractable algorithms to compute simple and tight overapproximations of SME in the form of minimum enclosing ellipsoids (MEE). We first introduce the hierarchy of enclosing ellipsoids proposed by Nie and Demmel (2005), based on sums-ofsquares relaxations, that asymptotically converge to the MEE of a basic semialgebraic set. This framework, however, struggles in modern control and perception problems due to computational challenges. We contribute three computational enhancements to make this framework practical, namely constraints pruning, generalized relaxed Chebyshev center, and handling non-Euclidean geometry. We showcase numerical examples on system identification and object pose estimation.

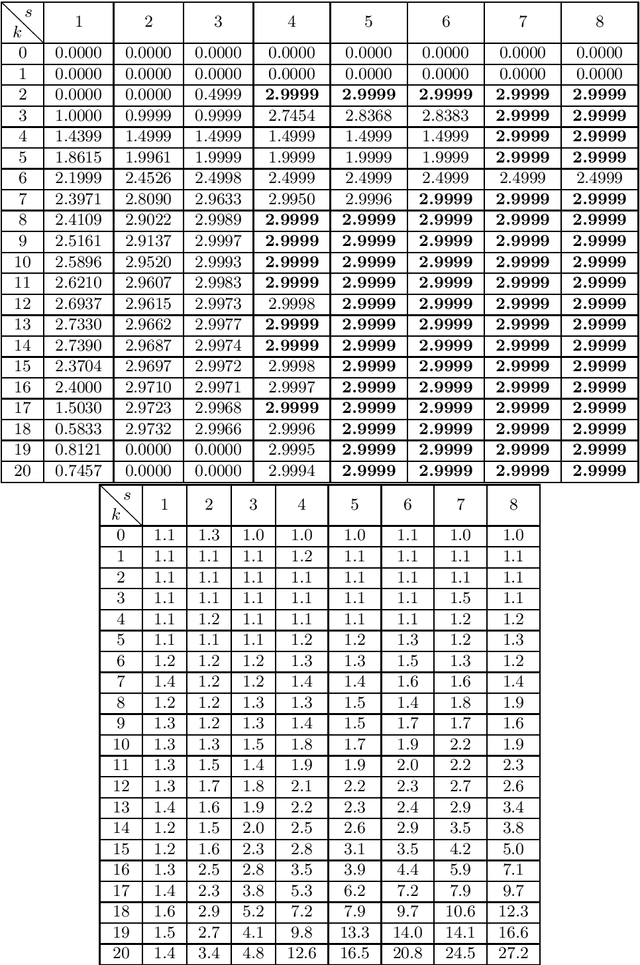
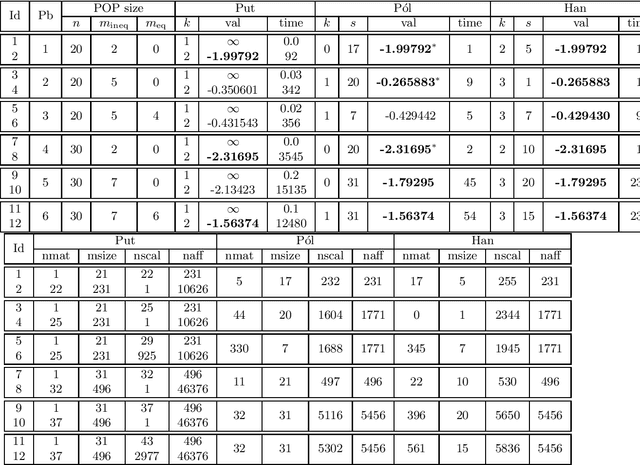
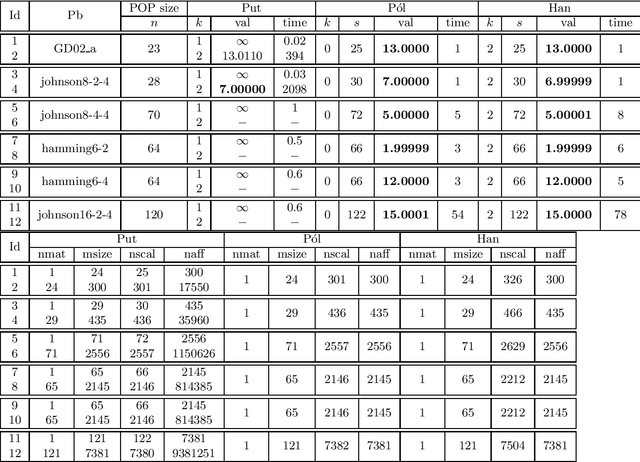
Tractable hierarchies of convex relaxations for polynomial optimization on the nonnegative orthant

We consider polynomial optimization problems (POP) on a semialgebraic set contained in the nonnegative orthant (every POP on a compact set can be put in this format by a simple translation of the origin). Such a POP can be converted to an equivalent POP by squaring each variable. Using even symmetry and the concept of factor width, we propose a hierarchy of semidefinite relaxations based on the extension of P\'olya's Positivstellensatz by Dickinson-Povh. As its distinguishing and crucial feature, the maximal matrix size of each resulting semidefinite relaxation can be chosen arbitrarily and in addition, we prove that the sequence of values returned by the new hierarchy converges to the optimal value of the original POP at the rate $O(\varepsilon^{-c})$ if the semialgebraic set has nonempty interior. When applied to (i) robustness certification of multi-layer neural networks and (ii) computation of positive maximal singular values, our method based on P\'olya's Positivstellensatz provides better bounds and runs several hundred times faster than the standard Moment-SOS hierarchy.

Polynomial Optimization for Bounding Lipschitz Constants of Deep Networks

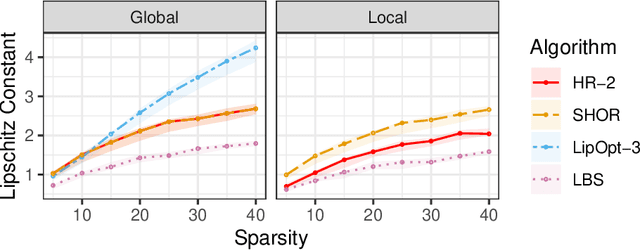
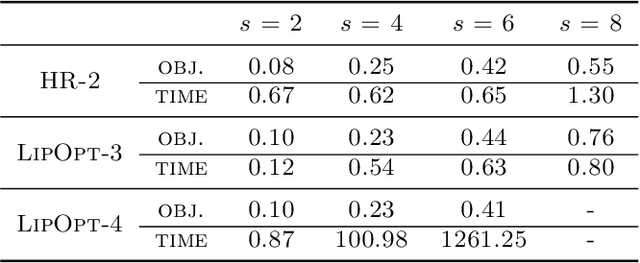
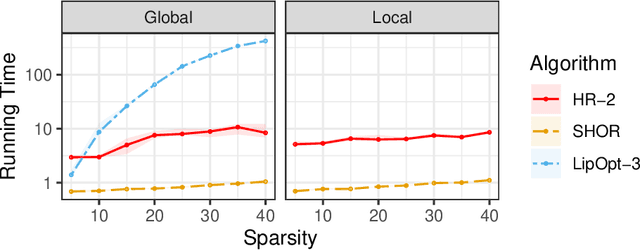
The Lipschitz constant of a network plays an important role in many applications of deep learning, such as robustness certification and Wasserstein Generative Adversarial Network. We introduce a semidefinite programming hierarchy to estimate the global and local Lipschitz constant of a multiple layer deep neural network. The novelty is to combine a polynomial lifting for ReLU functions derivatives with a weak generalization of Putinar's positivity certificate. This idea could also apply to other, nearly sparse, polynomial optimization problems in machine learning. We empirically demonstrate that our method not only runs faster than state-of-the-art linear programming based method, but also provides sharper bounds.

Data analysis from empirical moments and the Christoffel function

Spectral features of the empirical moment matrix constitute a resourceful tool for unveiling properties of a cloud of points, among which, density, support and latent structures. It is already well known that the empirical moment matrix encodes a great deal of subtle attributes of the underlying measure. Starting from this object as base of observations we combine ideas from statistics, real algebraic geometry, orthogonal polynomials and approximation theory for opening new insights relevant for Machine Learning (ML) problems with data supported on singular sets. Refined concepts and results from real algebraic geometry and approximation theory are empowering a simple tool (the empirical moment matrix) for the task of solving non-trivial questions in data analysis. We provide (1) theoretical support, (2) numerical experiments and, (3) connections to real world data as a validation of the stamina of the empirical moment matrix approach.

The empirical Christoffel function with applications in Machine Learning

We illustrate the potential applications in machine learning of the Christoffel function, or more precisely, its empirical counterpart associated with a counting measure uniformly supported on a finite set of points. Firstly, we provide a thresholding scheme which allows to approximate the support of a measure from a finite subset of its moments with strong asymptotic guaranties. Secondly, we provide a consistency result which relates the empirical Christoffel function and its population counterpart in the limit of large samples. Finally, we illustrate the relevance of our results on simulated and real world datasets for several applications in statistics and machine learning: (a) density and support estimation from finite samples, (b) outlier and novelty detection and (c) affine matching.

Sorting out typicality with the inverse moment matrix SOS polynomial

We study a surprising phenomenon related to the representation of a cloud of data points using polynomials. We start with the previously unnoticed empirical observation that, given a collection (a cloud) of data points, the sublevel sets of a certain distinguished polynomial capture the shape of the cloud very accurately. This distinguished polynomial is a sum-of-squares (SOS) derived in a simple manner from the inverse of the empirical moment matrix. In fact, this SOS polynomial is directly related to orthogonal polynomials and the Christoffel function. This allows to generalize and interpret extremality properties of orthogonal polynomials and to provide a mathematical rationale for the observed phenomenon. Among diverse potential applications, we illustrate the relevance of our results on a network intrusion detection task for which we obtain performances similar to existing dedicated methods reported in the literature.

Approximating Pareto Curves using Semidefinite Relaxations

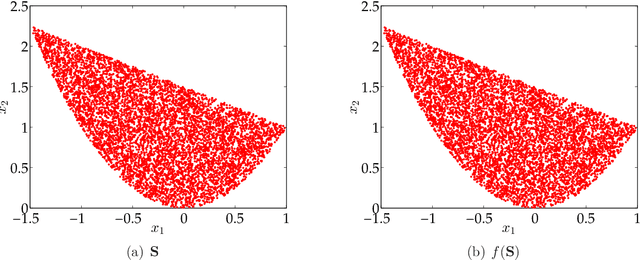
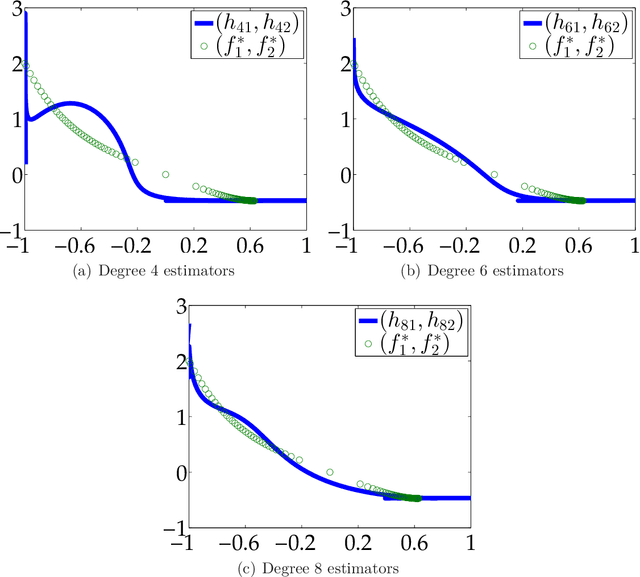
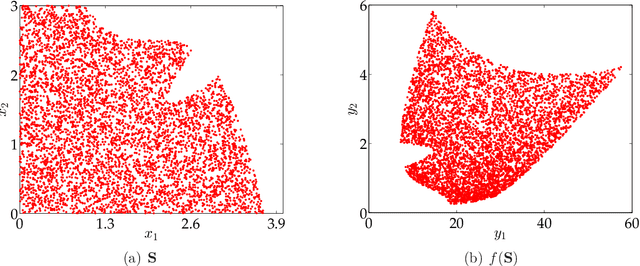
We consider the problem of constructing an approximation of the Pareto curve associated with the multiobjective optimization problem $\min_{\mathbf{x} \in \mathbf{S}}\{ (f_1(\mathbf{x}), f_2(\mathbf{x})) \}$, where $f_1$ and $f_2$ are two conflicting polynomial criteria and $\mathbf{S} \subset \mathbb{R}^n$ is a compact basic semialgebraic set. We provide a systematic numerical scheme to approximate the Pareto curve. We start by reducing the initial problem into a scalarized polynomial optimization problem (POP). Three scalarization methods lead to consider different parametric POPs, namely (a) a weighted convex sum approximation, (b) a weighted Chebyshev approximation, and (c) a parametric sublevel set approximation. For each case, we have to solve a semidefinite programming (SDP) hierarchy parametrized by the number of moments or equivalently the degree of a polynomial sums of squares approximation of the Pareto curve. When the degree of the polynomial approximation tends to infinity, we provide guarantees of convergence to the Pareto curve in $L^2$-norm for methods (a) and (b), and $L^1$-norm for method (c).