Polynomial Optimization for Bounding Lipschitz Constants of Deep Networks

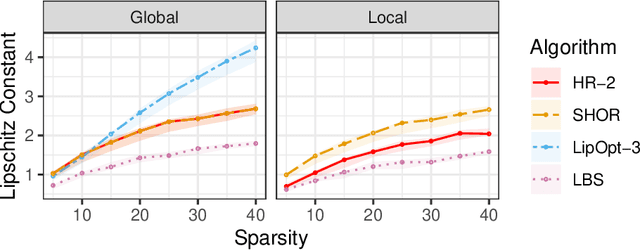
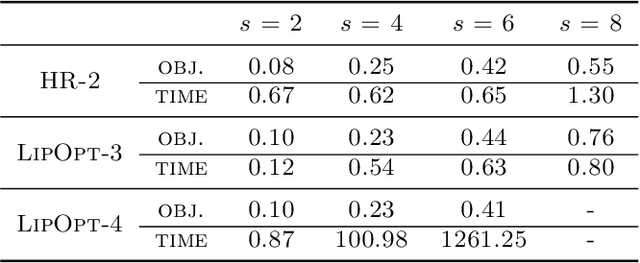
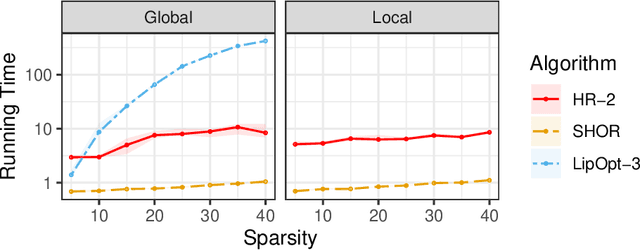
The Lipschitz constant of a network plays an important role in many applications of deep learning, such as robustness certification and Wasserstein Generative Adversarial Network. We introduce a semidefinite programming hierarchy to estimate the global and local Lipschitz constant of a multiple layer deep neural network. The novelty is to combine a polynomial lifting for ReLU functions derivatives with a weak generalization of Putinar's positivity certificate. This idea could also apply to other, nearly sparse, polynomial optimization problems in machine learning. We empirically demonstrate that our method not only runs faster than state-of-the-art linear programming based method, but also provides sharper bounds.