Globally Optimal Solution to Inverse Kinematics of 7DOF Serial Manipulator
Paper and Code
Jul 24, 2020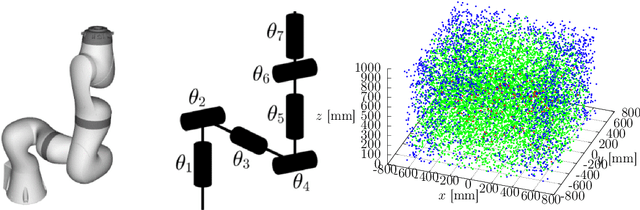

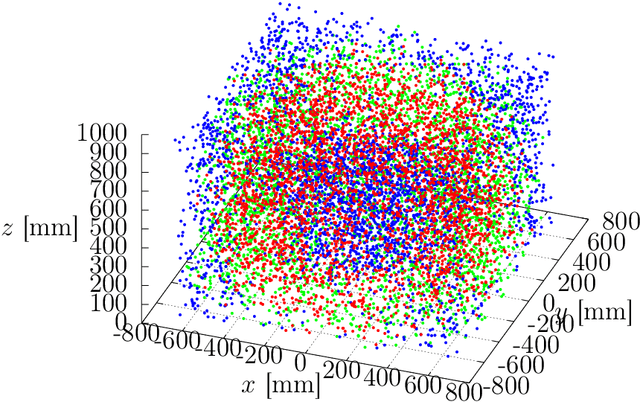
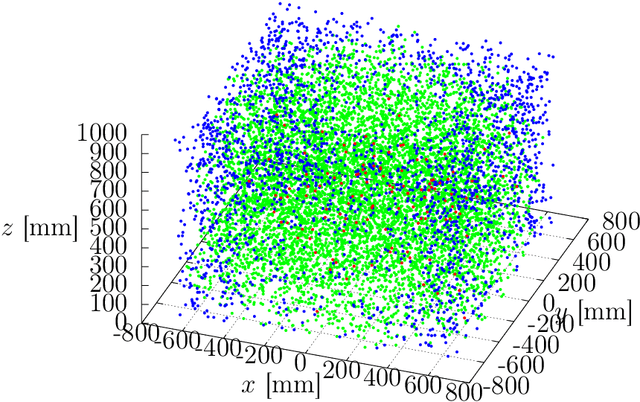
The Inverse Kinematics (IK) problem is to nd robot control parameters to bring it into the desired position under the kinematics and collision constraints. We present a global solution to the optimal IK problem for a general serial 7DOF manipulator with revolute joints and a quadratic polynomial objective function. We show that the kinematic constraints due to rotations can all be generated by second-degree polynomials. This is important since it signicantly simplies further step where we nd the optimal solution by Lasserre relaxations of non-convex polynomial systems. We demonstrate that the second relaxation is sucient to solve the 7DOF IK problem. Our approach is certiably globally optimal. We demonstrate the method on the 7DOF KUKA LBR IIWA manipulator and show that we are able to compute the optimal IK or certify in-feasibility in 99 % tested poses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge