Pub-Guard-LLM: Detecting Fraudulent Biomedical Articles with Reliable Explanations

A significant and growing number of published scientific articles is found to involve fraudulent practices, posing a serious threat to the credibility and safety of research in fields such as medicine. We propose Pub-Guard-LLM, the first large language model-based system tailored to fraud detection of biomedical scientific articles. We provide three application modes for deploying Pub-Guard-LLM: vanilla reasoning, retrieval-augmented generation, and multi-agent debate. Each mode allows for textual explanations of predictions. To assess the performance of our system, we introduce an open-source benchmark, PubMed Retraction, comprising over 11K real-world biomedical articles, including metadata and retraction labels. We show that, across all modes, Pub-Guard-LLM consistently surpasses the performance of various baselines and provides more reliable explanations, namely explanations which are deemed more relevant and coherent than those generated by the baselines when evaluated by multiple assessment methods. By enhancing both detection performance and explainability in scientific fraud detection, Pub-Guard-LLM contributes to safeguarding research integrity with a novel, effective, open-source tool.

A unifying approach on bias and variance analysis for classification

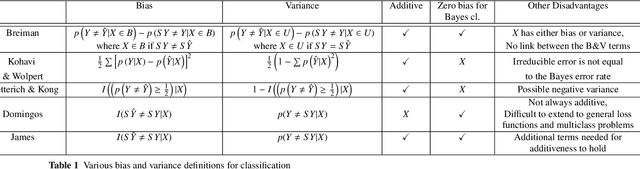
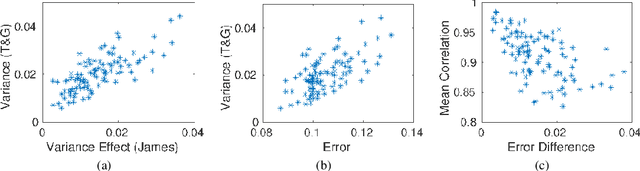
Standard bias and variance (B&V) terminologies were originally defined for the regression setting and their extensions to classification have led to several different models / definitions in the literature. In this paper, we aim to provide the link between the commonly used frameworks of Tumer & Ghosh (T&G) and James. By unifying the two approaches, we relate the B&V defined for the 0/1 loss to the standard B&V of the boundary distributions given for the squared error loss. The closed form relationships provide a deeper understanding of classification performance, and their use is demonstrated in two case studies.

ECOC as a Method of Constructing Deep Convolutional Neural Network Ensembles

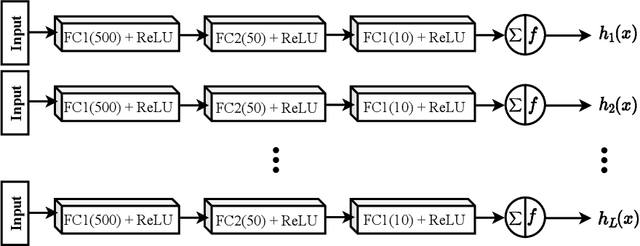
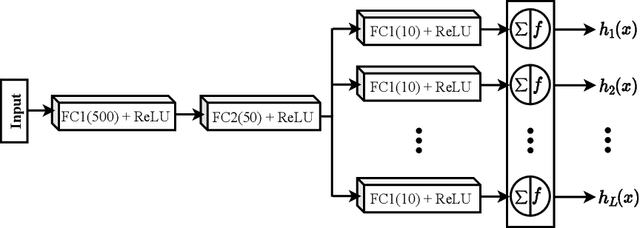
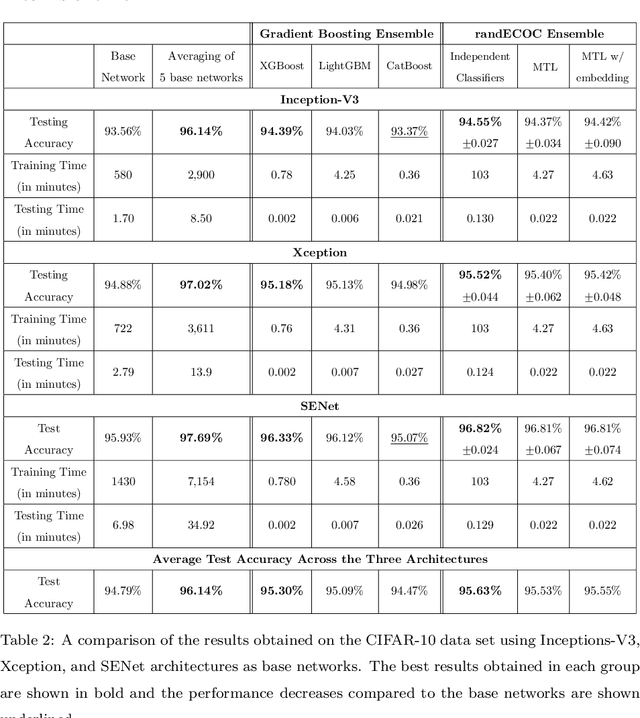
Deep neural networks have enhanced the performance of decision making systems in many applications including image understanding, and further gains can be achieved by constructing ensembles. However, designing an ensemble of deep networks is often not very beneficial since the time needed to train the constituent networks is very high or the performance gain obtained is not very significant. In this paper, we analyse error correcting output coding (ECOC) framework to be used as an ensemble technique for deep networks and propose different design strategies to address the accuracy-complexity trade-off. We carry out an extensive comparative study between the introduced ECOC designs and the state-of-the-art ensemble techniques such as ensemble averaging and gradient boosting decision trees. Furthermore, we propose a combinatory technique which is shown to reveal the highest classification performance amongst all.

Delta divergence: A novel decision cognizant measure of classifier incongruence

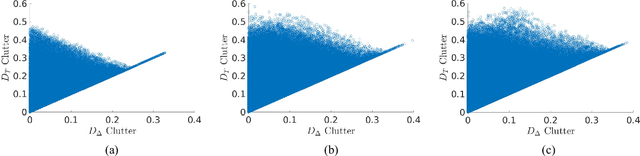
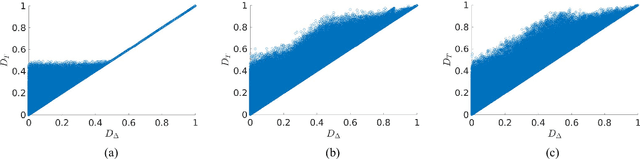
Disagreement between two classifiers regarding the class membership of an observation in pattern recognition can be indicative of an anomaly and its nuance. As in general classifiers base their decision on class aposteriori probabilities, the most natural approach to detecting classifier incongruence is to use divergence. However, existing divergences are not particularly suitable to gauge classifier incongruence. In this paper, we postulate the properties that a divergence measure should satisfy and propose a novel divergence measure, referred to as Delta divergence. In contrast to existing measures, it is decision cognizant. The focus in Delta divergence on the dominant hypotheses has a clutter reducing property, the significance of which grows with increasing number of classes. The proposed measure satisfies other important properties such as symmetry, and independence of classifier confidence. The relationship of the proposed divergence to some baseline measures is demonstrated experimentally, showing its superiority.