Delta divergence: A novel decision cognizant measure of classifier incongruence
Paper and Code
Jul 04, 2016
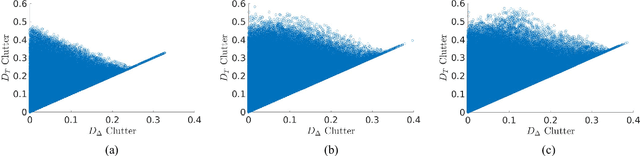
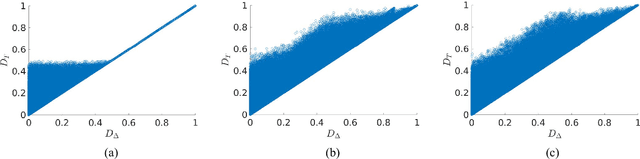

Disagreement between two classifiers regarding the class membership of an observation in pattern recognition can be indicative of an anomaly and its nuance. As in general classifiers base their decision on class aposteriori probabilities, the most natural approach to detecting classifier incongruence is to use divergence. However, existing divergences are not particularly suitable to gauge classifier incongruence. In this paper, we postulate the properties that a divergence measure should satisfy and propose a novel divergence measure, referred to as Delta divergence. In contrast to existing measures, it is decision cognizant. The focus in Delta divergence on the dominant hypotheses has a clutter reducing property, the significance of which grows with increasing number of classes. The proposed measure satisfies other important properties such as symmetry, and independence of classifier confidence. The relationship of the proposed divergence to some baseline measures is demonstrated experimentally, showing its superiority.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge