EarthDial: Turning Multi-sensory Earth Observations to Interactive Dialogues

Automated analysis of vast Earth observation data via interactive Vision-Language Models (VLMs) can unlock new opportunities for environmental monitoring, disaster response, and resource management. Existing generic VLMs do not perform well on Remote Sensing data, while the recent Geo-spatial VLMs remain restricted to a fixed resolution and few sensor modalities. In this paper, we introduce EarthDial, a conversational assistant specifically designed for Earth Observation (EO) data, transforming complex, multi-sensory Earth observations into interactive, natural language dialogues. EarthDial supports multi-spectral, multi-temporal, and multi-resolution imagery, enabling a wide range of remote sensing tasks, including classification, detection, captioning, question answering, visual reasoning, and visual grounding. To achieve this, we introduce an extensive instruction tuning dataset comprising over 11.11M instruction pairs covering RGB, Synthetic Aperture Radar (SAR), and multispectral modalities such as Near-Infrared (NIR) and infrared. Furthermore, EarthDial handles bi-temporal and multi-temporal sequence analysis for applications like change detection. Our extensive experimental results on 37 downstream applications demonstrate that EarthDial outperforms existing generic and domain-specific models, achieving better generalization across various EO tasks.

Multiscale Neural Operator: Learning Fast and Grid-independent PDE Solvers

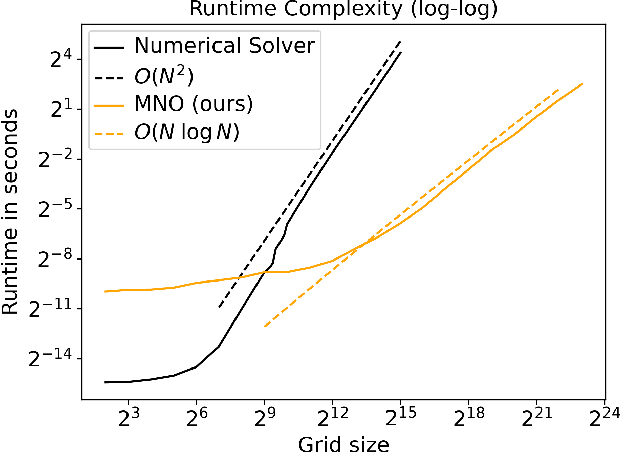
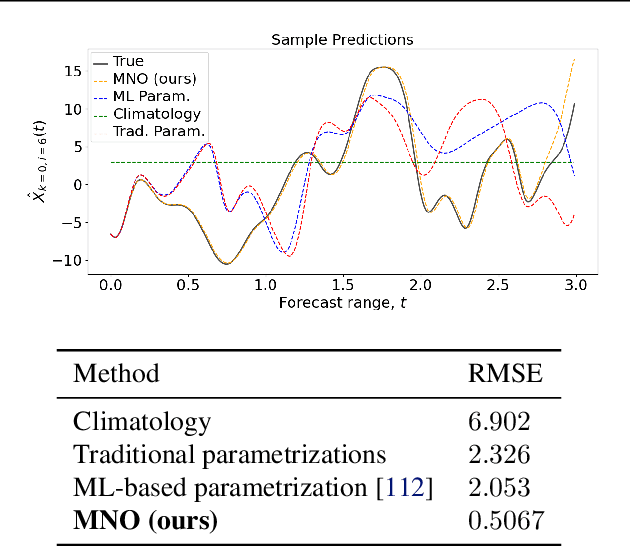
Numerical simulations in climate, chemistry, or astrophysics are computationally too expensive for uncertainty quantification or parameter-exploration at high-resolution. Reduced-order or surrogate models are multiple orders of magnitude faster, but traditional surrogates are inflexible or inaccurate and pure machine learning (ML)-based surrogates too data-hungry. We propose a hybrid, flexible surrogate model that exploits known physics for simulating large-scale dynamics and limits learning to the hard-to-model term, which is called parametrization or closure and captures the effect of fine- onto large-scale dynamics. Leveraging neural operators, we are the first to learn grid-independent, non-local, and flexible parametrizations. Our \textit{multiscale neural operator} is motivated by a rich literature in multiscale modeling, has quasilinear runtime complexity, is more accurate or flexible than state-of-the-art parametrizations and demonstrated on the chaotic equation multiscale Lorenz96.