Data Augmentation for Automated Adaptive Rodent Training

Fully optimized automation of behavioral training protocols for lab animals like rodents has long been a coveted goal for researchers. It is an otherwise labor-intensive and time-consuming process that demands close interaction between the animal and the researcher. In this work, we used a data-driven approach to optimize the way rodents are trained in labs. In pursuit of our goal, we looked at data augmentation, a technique that scales well in data-poor environments. Using data augmentation, we built several artificial rodent models, which in turn would be used to build an efficient and automatic trainer. Then we developed a novel similarity metric based on the action probability distribution to measure the behavioral resemblance of our models to that of real rodents.

Screw Geometry Meets Bandits: Incremental Acquisition of Demonstrations to Generate Manipulation Plans

In this paper, we study the problem of methodically obtaining a sufficient set of kinesthetic demonstrations, one at a time, such that a robot can be confident of its ability to perform a complex manipulation task in a given region of its workspace. Although Learning from Demonstrations has been an active area of research, the problems of checking whether a set of demonstrations is sufficient, and systematically seeking additional demonstrations have remained open. We present a novel approach to address these open problems using (i) a screw geometric representation to generate manipulation plans from demonstrations, which makes the sufficiency of a set of demonstrations measurable; (ii) a sampling strategy based on PAC-learning from multi-armed bandit optimization to evaluate the robot's ability to generate manipulation plans in a subregion of its task space; and (iii) a heuristic to seek additional demonstration from areas of weakness. Thus, we present an approach for the robot to incrementally and actively ask for new demonstration examples until the robot can assess with high confidence that it can perform the task successfully. We present experimental results on two example manipulation tasks, namely, pouring and scooping, to illustrate our approach. A short video on the method: https://youtu.be/R-qICICdEos

Value of Information in Probabilistic Logic Programs

In medical decision making, we have to choose among several expensive diagnostic tests such that the certainty about a patient's health is maximized while remaining within the bounds of resources like time and money. The expected increase in certainty in the patient's condition due to performing a test is called the value of information (VoI) for that test. In general, VoI relates to acquiring additional information to improve decision-making based on probabilistic reasoning in an uncertain system. This paper presents a framework for acquiring information based on VoI in uncertain systems modeled as Probabilistic Logic Programs (PLPs). Optimal decision-making in uncertain systems modeled as PLPs have already been studied before. But, acquiring additional information to further improve the results of making the optimal decision has remained open in this context. We model decision-making in an uncertain system with a PLP and a set of top-level queries, with a set of utility measures over the distributions of these queries. The PLP is annotated with a set of atoms labeled as "observable"; in the medical diagnosis example, the observable atoms will be results of diagnostic tests. Each observable atom has an associated cost. This setting of optimally selecting observations based on VoI is more general than that considered by any prior work. Given a limited budget, optimally choosing observable atoms based on VoI is intractable in general. We give a greedy algorithm for constructing a "conditional plan" of observations: a schedule where the selection of what atom to observe next depends on earlier observations. We show that, preempting the algorithm anytime before completion provides a usable result, the result improves over time, and, in the absence of a well-defined budget, converges to the optimal solution.

Inference in Probabilistic Logic Programs using Lifted Explanations

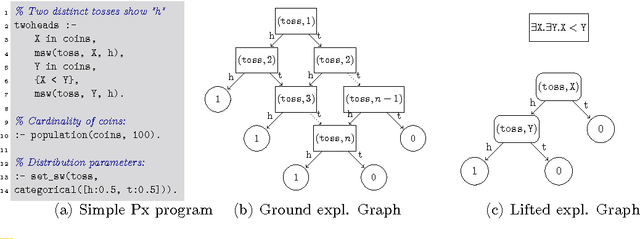
In this paper, we consider the problem of lifted inference in the context of Prism-like probabilistic logic programming languages. Traditional inference in such languages involves the construction of an explanation graph for the query and computing probabilities over this graph. When evaluating queries over probabilistic logic programs with a large number of instances of random variables, traditional methods treat each instance separately. For many programs and queries, we observe that explanations can be summarized into substantially more compact structures, which we call lifted explanation graphs. In this paper, we define lifted explanation graphs and operations over them. In contrast to existing lifted inference techniques, our method for constructing lifted explanations naturally generalizes existing methods for constructing explanation graphs. To compute probability of query answers, we solve recurrences generated from the lifted graphs. We show examples where the use of our technique reduces the asymptotic complexity of inference.

Adaptive MCMC-Based Inference in Probabilistic Logic Programs

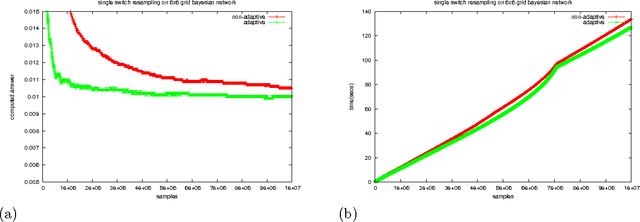
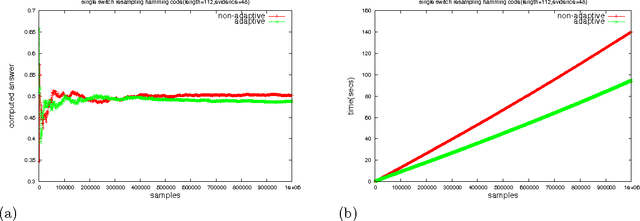
Probabilistic Logic Programming (PLP) languages enable programmers to specify systems that combine logical models with statistical knowledge. The inference problem, to determine the probability of query answers in PLP, is intractable in general, thereby motivating the need for approximate techniques. In this paper, we present a technique for approximate inference of conditional probabilities for PLP queries. It is an Adaptive Markov Chain Monte Carlo (MCMC) technique, where the distribution from which samples are drawn is modified as the Markov Chain is explored. In particular, the distribution is progressively modified to increase the likelihood that a generated sample is consistent with evidence. In our context, each sample is uniquely characterized by the outcomes of a set of random variables. Inspired by reinforcement learning, our technique propagates rewards to random variable/outcome pairs used in a sample based on whether the sample was consistent or not. The cumulative rewards of each outcome is used to derive a new "adapted distribution" for each random variable. For a sequence of samples, the distributions are progressively adapted after each sample. For a query with "Markovian evaluation structure", we show that the adapted distribution of samples converges to the query's conditional probability distribution. For Markovian queries, we present a modified adaptation process that can be used in adaptive MCMC as well as adaptive independent sampling. We empirically evaluate the effectiveness of the adaptive sampling methods for queries with and without Markovian evaluation structure.

Inference in Probabilistic Logic Programs with Continuous Random Variables

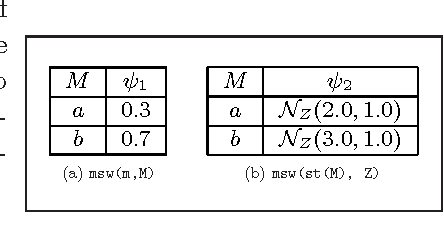
Probabilistic Logic Programming (PLP), exemplified by Sato and Kameya's PRISM, Poole's ICL, Raedt et al's ProbLog and Vennekens et al's LPAD, is aimed at combining statistical and logical knowledge representation and inference. A key characteristic of PLP frameworks is that they are conservative extensions to non-probabilistic logic programs which have been widely used for knowledge representation. PLP frameworks extend traditional logic programming semantics to a distribution semantics, where the semantics of a probabilistic logic program is given in terms of a distribution over possible models of the program. However, the inference techniques used in these works rely on enumerating sets of explanations for a query answer. Consequently, these languages permit very limited use of random variables with continuous distributions. In this paper, we present a symbolic inference procedure that uses constraints and represents sets of explanations without enumeration. This permits us to reason over PLPs with Gaussian or Gamma-distributed random variables (in addition to discrete-valued random variables) and linear equality constraints over reals. We develop the inference procedure in the context of PRISM; however the procedure's core ideas can be easily applied to other PLP languages as well. An interesting aspect of our inference procedure is that PRISM's query evaluation process becomes a special case in the absence of any continuous random variables in the program. The symbolic inference procedure enables us to reason over complex probabilistic models such as Kalman filters and a large subclass of Hybrid Bayesian networks that were hitherto not possible in PLP frameworks. (To appear in Theory and Practice of Logic Programming).

Parameter Learning in PRISM Programs with Continuous Random Variables

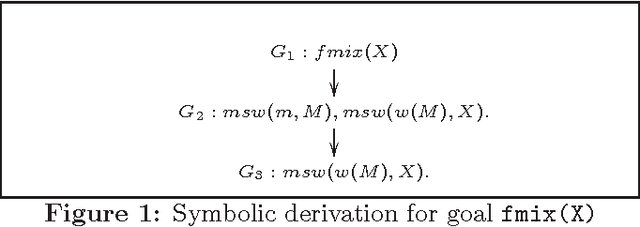
Probabilistic Logic Programming (PLP), exemplified by Sato and Kameya's PRISM, Poole's ICL, De Raedt et al's ProbLog and Vennekens et al's LPAD, combines statistical and logical knowledge representation and inference. Inference in these languages is based on enumerative construction of proofs over logic programs. Consequently, these languages permit very limited use of random variables with continuous distributions. In this paper, we extend PRISM with Gaussian random variables and linear equality constraints, and consider the problem of parameter learning in the extended language. Many statistical models such as finite mixture models and Kalman filter can be encoded in extended PRISM. Our EM-based learning algorithm uses a symbolic inference procedure that represents sets of derivations without enumeration. This permits us to learn the distribution parameters of extended PRISM programs with discrete as well as Gaussian variables. The learning algorithm naturally generalizes the ones used for PRISM and Hybrid Bayesian Networks.