Adaptive MCMC-Based Inference in Probabilistic Logic Programs
Paper and Code
Mar 24, 2014

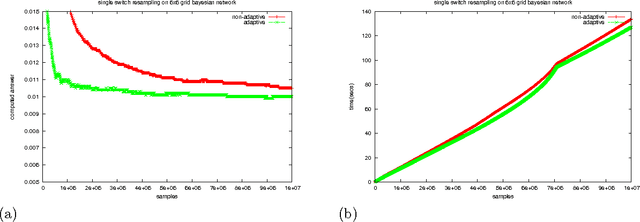
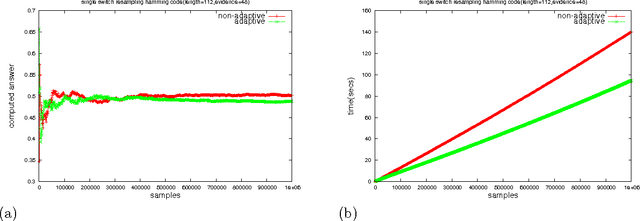
Probabilistic Logic Programming (PLP) languages enable programmers to specify systems that combine logical models with statistical knowledge. The inference problem, to determine the probability of query answers in PLP, is intractable in general, thereby motivating the need for approximate techniques. In this paper, we present a technique for approximate inference of conditional probabilities for PLP queries. It is an Adaptive Markov Chain Monte Carlo (MCMC) technique, where the distribution from which samples are drawn is modified as the Markov Chain is explored. In particular, the distribution is progressively modified to increase the likelihood that a generated sample is consistent with evidence. In our context, each sample is uniquely characterized by the outcomes of a set of random variables. Inspired by reinforcement learning, our technique propagates rewards to random variable/outcome pairs used in a sample based on whether the sample was consistent or not. The cumulative rewards of each outcome is used to derive a new "adapted distribution" for each random variable. For a sequence of samples, the distributions are progressively adapted after each sample. For a query with "Markovian evaluation structure", we show that the adapted distribution of samples converges to the query's conditional probability distribution. For Markovian queries, we present a modified adaptation process that can be used in adaptive MCMC as well as adaptive independent sampling. We empirically evaluate the effectiveness of the adaptive sampling methods for queries with and without Markovian evaluation structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge